សៀវភៅខ្លែង គណិតវិទ្យាទី៣ វគ្គទី១ កំណត់ចតុកោណកែងជារាងបួនជ្រុង ជ្រុងវែងស្មើគ្នា ២ជ្រុង និងជ្រុងខ្លីស្មើគ្នា។

ចតុកោណកែងមានលក្ខណៈសម្បត្តិទាំងអស់នៃ isosceles trapezoid និង parallelogram ដូចជា៖
- គូនៃភាគីទល់មុខគឺតែងតែស្របគ្នានិងស្មើគ្នា។
- មុំស្មើគ្នានិង 90 ដឺក្រេ។
- ចតុកោណមានស៊ីមេទ្រីតាមអង្កត់ទ្រូង និងកាត់ចំណុចកណ្តាលនៃភាគី។
- ចតុកោណកែងដែលមានមុំបីជាចតុកោណកែង។
- isosceles trapezoid ដែលមានមុំខាងស្តាំមួយគឺជាចតុកោណ។
- ប្រលេឡូក្រាមដែលមានមុំខាងស្តាំមួយគឺជាចតុកោណកែង។
- មុខដែលមានអង្កត់ទ្រូងស្មើគ្នាពីរគឺចតុកោណ។
យោងតាមសៀវភៅគណិតវិទ្យាទី៣ ដើម្បីគណនាបរិវេណនៃចតុកោណ យើងយកប្រវែងបូកទទឹង (ឯកតារង្វាស់ដូចគ្នា) រួចគុណនឹង ២។
| P = (a+b) x 2 |
នៅក្នុងនោះ។
P គឺជាបរិវេណនៃចតុកោណកែង។
a គឺជាប្រវែងនៃចតុកោណ។
b គឺជាទទឹងនៃចតុកោណកែង។

ឧទាហរណ៍៖ គណនាបរិវេណនៃចតុកោណកែងដែលមានប្រវែង 6cm និងទទឹង 4cm។
ចំលើយ៖ បរិវេណនៃចតុកោណគឺ P = (6+4) x 2 = 20 (cm) ។
ប្រៀបធៀបចតុកោណកែង និងការ៉េ
| លក្ខណៈវិនិច្ឆ័យ | ចតុកោណ | ការ៉េ |
|---|---|---|
| គែម | 4 ជ្រុង, 2 គូនៃភាគីផ្ទុយគឺស្មើគ្នា | ៤ ជ្រុង ទាំង ៤ ស្មើ |
| ជ្រុង | 4 មុំខាងស្តាំ | 4 មុំខាងស្តាំ |
| អង្កត់ទ្រូង | អង្កត់ទ្រូងពីរគឺស្មើគ្នា ប្រសព្វគ្នាត្រង់ចំណុចកណ្តាល ប៉ុន្តែមិនកាត់កែងទេ។ | អង្កត់ទ្រូងពីរគឺស្មើគ្នា ប្រសព្វគ្នាត្រង់ចំណុចកណ្តាល ហើយកាត់កែងទៅគ្នាទៅវិញទៅមក។ |
| រូបមន្តសម្រាប់គណនាបរិវេណ | P = (a+b) x 2 | P = 4a |
| រូបមន្តសម្រាប់គណនាផ្ទៃដី | S = axb | S = a2 |
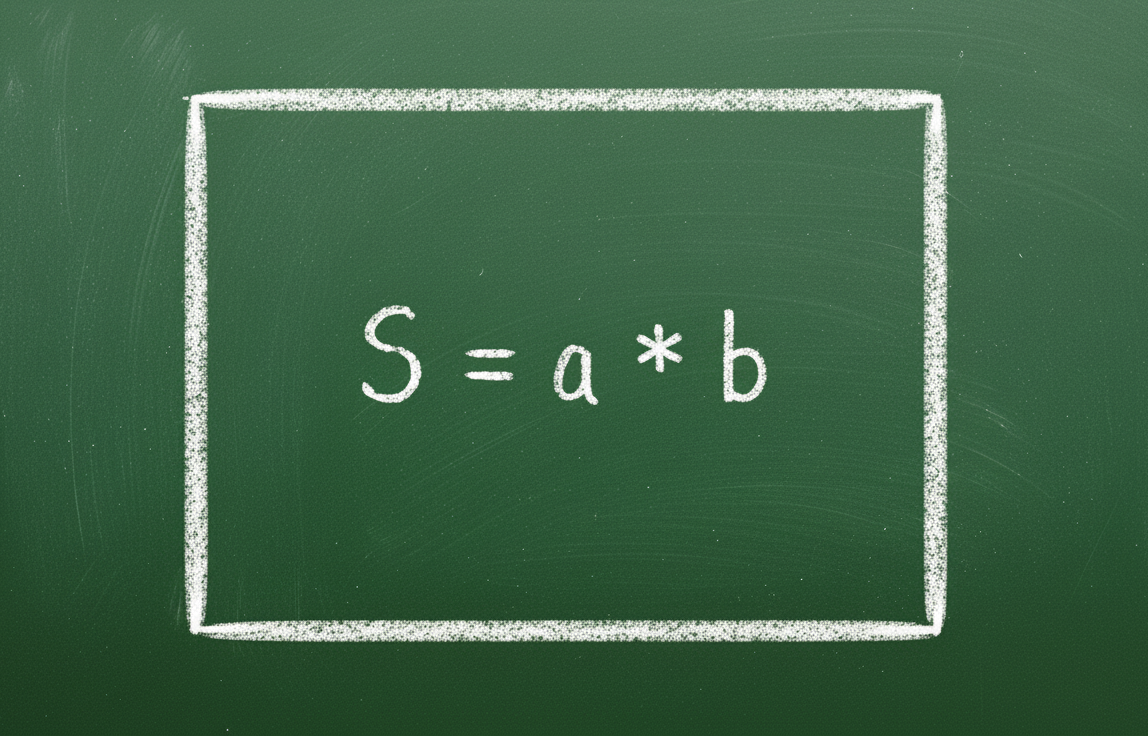
ប្រភព៖ https://vietnamnet.vn/cong-thuc-tinh-chu-vi-hinh-chu-nhat-la-gi-2452851.html


![[រូបថត] ពិធីបិទមហាសន្និបាតលើកទី១៨ គណៈកម្មាធិការបក្សទីក្រុងហាណូយ](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/17/1760704850107_ndo_br_1-jpg.webp)
![[រូបថត] ជ្រមុជខ្លួនអ្នកនៅក្នុងពិភពតន្ត្រីចម្រុះពណ៌នៃ "Secret Garden Live in Vietnam"](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760805978427_ndo_br_thiet-ke-chua-co-ten-41-png.webp)


![[រូបថត] ការប្រមូលកាកសំណល់ ការសាបព្រួសគ្រាប់ពូជពណ៌បៃតង](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760786475497_ndo_br_1-jpg.webp)
![[រូបថត] អគ្គលេខាបក្ស To Lam ចូលរួមពិធីរំលឹកខួបលើកទី 95 នៃទិវាប្រពៃណីរបស់មជ្ឈិមបក្ស](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760784671836_a1-bnd-4476-1940-jpg.webp)



























































































Kommentar (0)