과학자들은 1세기 이상 지속된 고전 기하학 문제에 대한 해결책을 찾았습니다.

기하학 문제에 대한 그림입니다.

사우스 차이나 모닝 포스트에 따르면, 현재 뉴욕 대학교(미국) 쿠랑 수학 연구소의 준교수인 수학자 홍 왕과 그의 동료 조슈아 잘(캐나다 브리티시 컬럼비아 대학교)은 20~21세기의 가장 어려운 기하학 문제 중 하나인 3차원 공간에서의 카케야 추측을 해결했습니다.

홍왕은 중국 구이린에서 태어나 베이징 대학에서 공부한 후 미국에서 가르치고 연구했습니다.

이 문제는 1917년 일본 수학자 가케야 소이치가 "바늘을 180도 회전시키는 데 필요한 최소 면적은 얼마인가?"라는 질문을 던졌을 때 시작되었습니다. 이 최소 면적을 "가케야 집합"이라고 합니다.

2차원 공간에서 바늘을 돌려 원을 만드는 것은 쉽게 시각화할 수 있지만, 회전이 더 유연하다면(예: 회전하면서 바늘을 흔드는 경우) 바늘이 쓸어내는 영역은 더 작아질 수 있습니다.

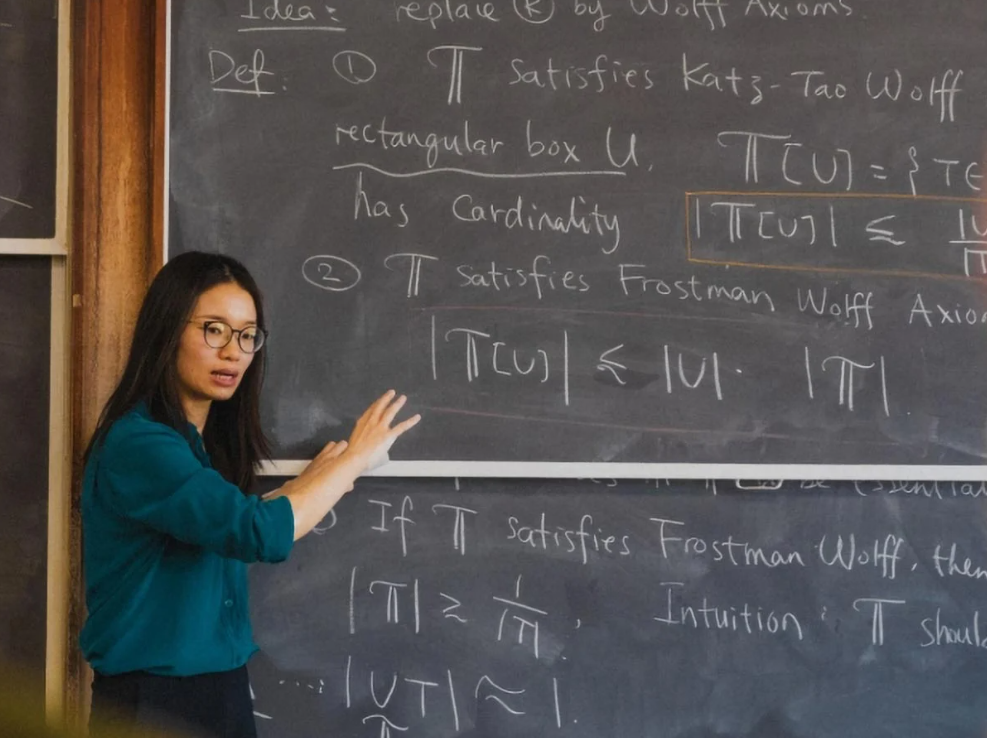
과학자들은 100년 이상 지속된 기하학 문제에 대한 해결책을 찾았습니다.

문제가 3차원으로 확대되면 문제는 훨씬 더 복잡해집니다. 카케야의 추측에 따르면 바늘을 모든 방향으로 회전시키려면 3차원 모두에서 충분한 공간이 필요하다. 즉, 너무 작거나 얇은 곳에 밀어 넣을 수 없다는 것이다.

왕과 잘은 arXiv 플랫폼에 최근 게재한 논문에서 3차원 공간에서 바늘을 회전시키는 영역은 명확한 모양을 가질 필요는 없지만 3차원 모두에서 충분히 커야 한다는 것을 보여주었습니다. 그 덕분에 그들은 이 문제를 해결했습니다. 이는 오늘날 수학에서 매우 중요한 발견으로 여겨집니다.

세계적인 수학자 중 한 명인 테렌스 타오 교수는 이를 "놀라운 발전"이라고 불렀습니다. 전문가들은 이 작업이 기하학에 대한 이해를 확장할 뿐만 아니라 이미지 처리, 무선 통신, 컴퓨터 과학, 암호화 등 공간의 움직임과 상호 작용을 이해하는 것이 매우 중요한 여러 분야에도 영향을 미칠 수 있다고 말했습니다.

"과장이기는 하지만, 이것은 우리가 수백 년 동안 기다려온 희귀한 해결책입니다." 라고 미국 라이스 대학교에서 수학을 가르치는 넷츠 카츠 교수가 말했습니다.

매사추세츠 공과대학(미국)의 강사인 거스 래리 교수에 따르면, 카케야 가설은 기하학 분야에서 더 큰 가설들의 "타워"를 형성하는 토대입니다. 이 가설을 풀면 지식의 탑의 더 높은 레벨에 접근하여 정복할 기회가 생깁니다.

"저는 이 문제가 간단하고 기본적인 기하학 문제라고 생각했지만, 실제로는 너무 어렵습니다. 이 문제는 수학계의 많은 저명한 학자들이 탐구해 왔지만, 대부분은 미미한 성과만 얻었고 체계적이지 못했으며 완전한 해법으로 여겨질 수 없었습니다."라고 거스 래리 교수는 말했습니다.

Phuong Anh (출처: 사이언스 데일리, SCMP)

출처: https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-geometry-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html