ຮູບສີ່ຫລ່ຽມແມ່ນຫຍັງ?
ຕາມບົດຮຽນທີ 13, ເລກທີ 8 (ຊຸດທີ 1) ຂອງບົດຮຽນ “ເຊື່ອມຕໍ່ຄວາມຮູ້ກັບຊີວິດ” ຂອງສຳນັກພິມ ສຶກສາ ຫວຽດນາມ ໄດ້ໃຫ້ຄຳນິຍາມຮູບສີ່ຫລ່ຽມມຸມສາກເປັນສີ່ຫຼ່ຽມມຸມຂວາ.
ຄຸນສົມບັດຂອງຮູບສີ່ຫຼ່ຽມແມ່ນມັນມີ 2 ດ້ານກົງກັນຂ້າມຂະຫນານ, 2 ດ້ານກົງກັນຂ້າມເທົ່າທຽມກັນ, 2 ມຸມກົງກັນຂ້າມເທົ່າທຽມກັນ, 2 ເສັ້ນຂວາງເທົ່າທຽມກັນແລະຕັດກັນຢູ່ຈຸດກາງຂອງແຕ່ລະເສັ້ນ.
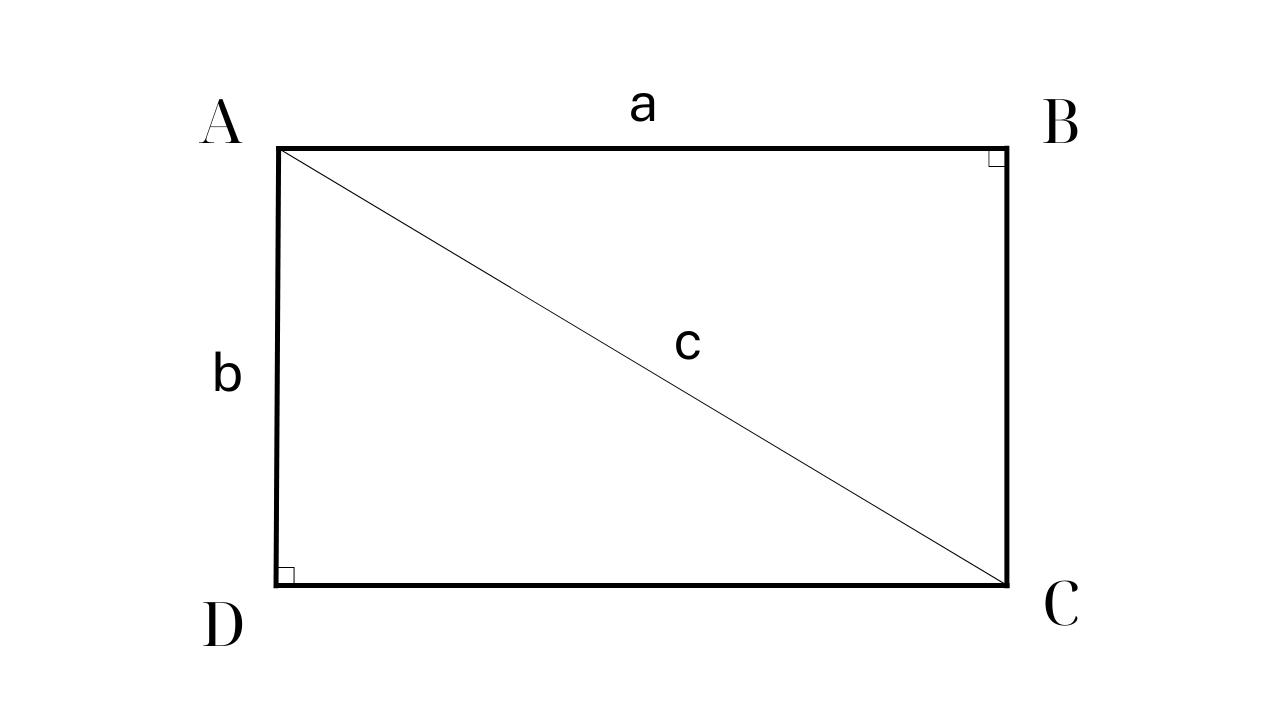
ສູດສໍາລັບການຄິດໄລ່ພື້ນທີ່ຂອງສີ່ຫລ່ຽມ
ໃນບົດຮຽນທີ 52, ປຶ້ມຄະນິດສາດ 3 (ເຫຼັ້ມທີ 2) ຂອງປຶ້ມແບບຮຽນ “ເຊື່ອມຕໍ່ຄວາມຮູ້ກັບຊີວິດ” ຂອງສຳນັກພິມເຜີຍແຜ່ສຶກສາຫວຽດນາມ, ສູດຄຳນວນພື້ນທີ່ຂອງສີ່ຫຼ່ຽມແມ່ນຄວາມຍາວຄູນກັບຄວາມກວ້າງ (ຫົວໜ່ວຍວັດແທກດຽວກັນ).
| S = axb |
ຢູ່ທີ່ນັ້ນ:
S: ພື້ນທີ່ຂອງສີ່ຫລ່ຽມ
a: ຄວາມຍາວຂອງສີ່ຫລ່ຽມ
b: ຄວາມກວ້າງຂອງສີ່ຫລ່ຽມ
ຕົວຢ່າງ: ກະດານໄມ້ຮູບສີ່ຫລ່ຽມທີ່ມີຄວາມກວ້າງ 5 ຊມແລະຍາວ 15 ຊມ. ຄິດໄລ່ພື້ນທີ່ຂອງກະດານໄມ້ນັ້ນ.
ຕອບ: ເນື້ອທີ່ຂອງກະດານໄມ້ແມ່ນ: S = 5 x 15 = 75 (ຊມ 2 )
ສູດການຄິດໄລ່ພື້ນທີ່ຂອງສີ່ຫລ່ຽມເມື່ອຮູ້ 1 ດ້ານແລະເສັ້ນຂວາງ
ເພື່ອຄິດໄລ່ພື້ນທີ່ຂອງສີ່ຫລ່ຽມເມື່ອຮູ້ເສັ້ນຂວາງແລະດ້ານຫນຶ່ງ, ມັນຈໍາເປັນຕ້ອງສົມທົບທິດສະດີ Pythagorean ກັບສູດພື້ນຖານ.
ຂັ້ນຕອນທີ 1: ນຳໃຊ້ທິດສະດີ Pythagorean ໃນສາມຫຼ່ຽມຂວາເພື່ອຄິດໄລ່ຄວາມຍາວຂອງດ້ານທີ່ຍັງເຫຼືອ.
ຂັ້ນຕອນທີ 2: ນໍາໃຊ້ສູດການຄິດໄລ່ພື້ນທີ່ຂອງສີ່ຫລ່ຽມ: S = axb
ຕົວຢ່າງ: ຮູບສີ່ຫລ່ຽມ ABCD ມີ AD = 60cm, ເສັ້ນຂວາງ AC ແມ່ນ 100cm. ຄິດໄລ່ພື້ນທີ່ຂອງ ABCD.
ຄໍາຕອບ:
ຂັ້ນຕອນທີ 1: ຊອກຫາດ້ານທີ່ຍັງເຫຼືອຂອງສີ່ຫລ່ຽມ ABCD ໂດຍໃຊ້ທິດສະດີ Pythagorean ໃນສາມຫຼ່ຽມຂວາ.
ຕາມນັ້ນ: AC 2 = AB 2 + AD 2 => AB 2 = AC 2 - AD 2 = 10000 - 3600 = 6400 => AB = 80 (ຊມ)
ຂັ້ນຕອນທີ 2: ພື້ນທີ່ ABCD = AB x AD = 60 x 80 = 4800 (ຊມ 2 )
ສູດສໍາລັບການຄິດໄລ່ພື້ນທີ່ຂອງສີ່ຫລ່ຽມໃນເວລາທີ່ຮູ້ perimeter
ເພື່ອຄິດໄລ່ພື້ນທີ່ຂອງຮູບສີ່ຫລ່ຽມເມື່ອຮູ້ perimeter, ທ່ານຕ້ອງສົມທົບສູດ perimeter ແລະສູດພື້ນຖານ.
ຂັ້ນຕອນທີ 1: ຈາກສູດການຄິດໄລ່ຂອບເຂດຂອງສີ່ຫລ່ຽມແມ່ນ P = (a + b) x 2 ມີ P ແມ່ນຂອບເຂດ, a ແມ່ນຄວາມຍາວ, b ແມ່ນຄວາມກວ້າງຂອງສີ່ຫລ່ຽມ, ພວກເຮົາມີ a = (P/2) - b ຫຼື b = (P/2) - a
ຂັ້ນຕອນທີ 2: ຫຼັງຈາກການຊອກຫາ a ຫຼື b, ນໍາໃຊ້ສູດການຄິດໄລ່ພື້ນທີ່ຂອງຮູບສີ່ແຈສາກຫນຶ່ງ: S = axb
ສັນຍານທີ່ຈະຮັບຮູ້ສີ່ຫລ່ຽມ?
ຕາມບົດຮຽນທີ 13, ເລກທີ 8 (ຊຸດທີ 1) ປຶ້ມແບບຮຽນ “ເຊື່ອມຕໍ່ຄວາມຮູ້ກັບຊີວິດ” ຂອງສຳນັກພິມສຶກສາຫວຽດນາມ, ບັນດາເຄື່ອງໝາຍທີ່ຈະຮັບຮູ້ຮູບສີ່ແຈສາກຄື:
- ສີ່ຫຼ່ຽມມີ 3 ມຸມຂວາ (ອີງຕາມນິຍາມ)
- ຮູບຂະໜານມີ 1 ມຸມຂວາ
- ຮູບຂະໜານມີສອງເສັ້ນຂວາງເທົ່າກັນ.
- isosceles trapezoid ມີມຸມຂວາຫນຶ່ງ.
ຮູບສີ່ຫຼ່ຽມຄຳເປັນຮູບຂະໜານບໍ?
ຕາມບົດຮຽນທີ 13, ເລກທີ 8 (ຊຸດທີ 1) ປຶ້ມແບບຮຽນ “ເຊື່ອມຕໍ່ຄວາມຮູ້ກັບຊີວິດ” ຂອງສຳນັກພິມສຶກສາຫວຽດນາມ, ຮູບສີ່ແຈສາກມີຄຸນສົມບັດທັງໝົດຂອງຂະໜານ. ດັ່ງນັ້ນ, ຮູບສີ່ຫລ່ຽມແມ່ນຮູບຂະຫນານພິເສດ.
ຮູບສີ່ຫຼ່ຽມມົນເປັນ isosceles trapezoid?
ບົດຮຽນທີ 13, ຄະນິດສາດ 8 (ຊຸດທີ 1) ປຶ້ມແບບຮຽນ “ເຊື່ອມຕໍ່ຄວາມຮູ້ກັບຊີວິດ” ຂອງສຳນັກພິມເຜີຍແຜ່ການສຶກສາ ຫວຽດນາມ, ຮູບສີ່ຫລ່ຽມມີຄຸນສົມບັດທັງໝົດຂອງຮູບຊົງ isosceles trapezoid. ດັ່ງນັ້ນ, ຮູບສີ່ຫລ່ຽມແມ່ນຮູບແບບພິເສດຂອງ isosceles trapezoid.
(ສັງເຄາະ)
ທີ່ມາ: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html


![[ຮູບພາບ] ໄຂກອງປະຊຸມໃຫຍ່ຄັ້ງທີ 12 ຂອງພັກການທະຫານສະໄໝທີ 2025-2030](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/30/2cd383b3130d41a1a4b5ace0d5eb989d)

![[ຮູບພາບ] ພາໂນຣາມາຂອງຂົວທີ່ພັກສາຍເຄເບີນ, ເປັນຂອດສຸດທ້າຍຂອງທາງດ່ວນ Ben Luc-Long Thanh](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/30/391fdf21025541d6b2f092e49a17243f)
![[ຮູບພາບ] ທ່ານປະທານປະເທດ ເຈືອງເຕີນຊາງ ຕ້ອນຮັບທ່ານປະທານສະພາແຫ່ງຊາດ ກູບາ Esteban Lazo Hernandez](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/30/4d38932911c24f6ea1936252bd5427fa)
![[ຮູບພາບ] ກອງປະຊຸມໃຫຍ່ຄັ້ງທີ 1 ຂອງອົງການພັກແຂວງ ຟູທໍ້ ສົກປີ 2025-2030](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/30/1507da06216649bba8a1ce6251816820)
![[ຮູບພາບ] ທ່ານເລຂາທິການໃຫຍ່ To Lam, ເລຂາທິການໃຫຍ່ການທະຫານສູນກາງເຂົ້າຮ່ວມກອງປະຊຸມໃຫຍ່ຄັ້ງທີ 12 ຂອງພັກກອມມູນິດຫວຽດນາມ](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/30/9b63aaa37ddb472ead84e3870a8ae825)


























































































(0)