১৭ বছর বয়সী মেয়ে ৪০ বছরের পুরনো গণিতের রহস্য সমাধান করেছে

ফেব্রুয়ারিতে, আন্তর্জাতিক গণিত সম্প্রদায় উত্তাল হয়ে ওঠে যখন একটি বৈজ্ঞানিক গবেষণাপত্র চার দশকেরও বেশি সময় ধরে সত্য বলে মনে হওয়া একটি বিখ্যাত অনুমানকে খণ্ডন করে।

লেখক কোনও অধ্যাপক বা অভিজ্ঞ গবেষক নন, বরং হান্না কায়রো - একজন ১৭ বছর বয়সী ছাত্রী।

কায়রো যে অনুমানকে প্রত্যাখ্যান করেছিল তাকে মিজোহাতা-তাকেউচি অনুমান বলা হত, যা সাইন তরঙ্গ থেকে ফাংশন তৈরির পদ্ধতি নিয়ে আলোচনা করত - যা সুরেলা বিশ্লেষণের ভিত্তি। বছরের পর বছর ধরে, গণিতবিদরা অনুমানটিকে সঠিক প্রমাণ করার চেষ্টা করছিলেন। কিন্তু কায়রো একটি পাল্টা যুক্তি খুঁজে পেয়েছিলেন: এটি ভুল ছিল। আবিষ্কারটি তাৎক্ষণিকভাবে আলোড়ন সৃষ্টি করে এবং একই সাথে জনসাধারণের সামনে একটি অসাধারণ তরুণ প্রতিভার নাম নিয়ে আসে।

হোমস্কুলিং থেকে স্নাতকোত্তর স্কুল পর্যন্ত

বাহামায় জন্মগ্রহণকারী হান্না তার দুই ভাইয়ের সাথেই বাড়িতেই পড়াশোনা করতেন। ১১ বছর বয়সের মধ্যে তিনি অনলাইন লেকচারের মাধ্যমে ক্যালকুলাস শেষ করেছিলেন এবং নিজে নিজে উন্নত বিশ্ববিদ্যালয়ের পাঠ্যপুস্তক আয়ত্ত করেছিলেন। কিন্তু বাড়িতে পড়াশোনা সীমাবদ্ধ এবং একাকী মনে হত। হান্নার কাছে গণিত বন্দিদশা থেকে মুক্তির জন্য একটি বিস্তৃত উন্মুক্ত জগৎ হয়ে ওঠে, যেখানে তিনি কেবল তার কল্পনাশক্তি দিয়ে যেকোনো সময় অন্বেষণ করতে পারতেন।

হান্না কায়রো বিশ্বাস করেন যে "গণিত একটি শিল্পরূপ।" (ছবি: সায়েন্টিফিক আমেরিকান)

কোভিড-১৯ মহামারীর কারণে পরিবারটি মার্কিন যুক্তরাষ্ট্রে আটকা পড়ে। এর ফলে হান্না বার্কলেতে ক্যালিফোর্নিয়া বিশ্ববিদ্যালয়ের গণিত ক্লাব এবং একটি অনলাইন গ্রীষ্মকালীন শিবিরে যোগদানের সুযোগ পান। তার ব্যাপক স্ব-অধ্যয়নের রেকর্ড অনুষদের শিক্ষার্থীদের মুগ্ধ করে, যার ফলে হান্না বার্কলে দ্বৈত-ডিগ্রি প্রোগ্রামে ভর্তির পথ প্রশস্ত করে, যেখানে তিনি উচ্চ বিদ্যালয়ের ডিপ্লোমা না থাকা সত্ত্বেও স্নাতক গণিতের ক্লাস নেওয়া শুরু করেন।

একটি অনুশীলনীতে, ২০০৮ সালের আন্তর্জাতিক গণিত অলিম্পিয়াডের স্বর্ণপদকপ্রাপ্ত এবং প্রিন্সটনের পিএইচডিধারী অধ্যাপক রুইশিয়াং ঝাং শিক্ষার্থীদের অনুশীলনের জন্য মিজোহাতা-তাকেউচি অনুমানের একটি সরলীকৃত সংস্করণ উপস্থাপন করেছিলেন। হান্না এখানেই থেমে থাকেননি: তিনি আরও গভীরভাবে খনন করতে থাকেন, অনেক ধারণা পরীক্ষা করেন এবং অবশেষে একটি পাল্টা যুক্তি খুঁজে পান যা মূল অনুমানকে ভেঙে দেয়। এই আবিষ্কার কেবল একটি ক্ষেত্রের দৃশ্যপটই বদলে দেয়নি, বরং অনেক সম্পর্কিত অনুমানেরও পতন ঘটায়।

এমনকি সেও প্রথমে সন্দেহবাদী ছিল। "আমি প্রায়শই মনে করি আমার কাছে একটি প্রমাণ আছে, কিন্তু পরে বুঝতে পারি যে এটি ভুল," কায়রো বলেন। কিন্তু এবার, দুটি জিনিস ভিন্ন ছিল: তিনি বুঝতে পেরেছিলেন যে তিনি এটিকে একটি সহজ কাঠামো দিয়ে প্রতিস্থাপন করতে পারেন যা এখনও একই ফলাফল দেবে, এবং আরও গুরুত্বপূর্ণ বিষয় হল, তিনি নিজেকে এবং অধ্যাপক ঝাং উভয়কেই বোঝাতে পেরেছিলেন যে প্রমাণটি সঠিক।

সকল সীমা ভেঙে ফেলো

কঠিন সমস্যা জয়ের জন্য কায়রোর যাত্রাও ছিল চ্যালেঞ্জিং। অভিজ্ঞতার অভাবের কারণে, তার প্রাথমিক প্রচেষ্টা প্রায়শই ত্রুটিপূর্ণ ছিল। "প্রতি সপ্তাহে আমি তার অফিসে একটি নতুন ধারণা নিয়ে আসতাম এবং জিজ্ঞাসা করতাম, 'এটা কি ঠিক?' এবং তিনি না বলতেন," কায়রো স্মরণ করেন।

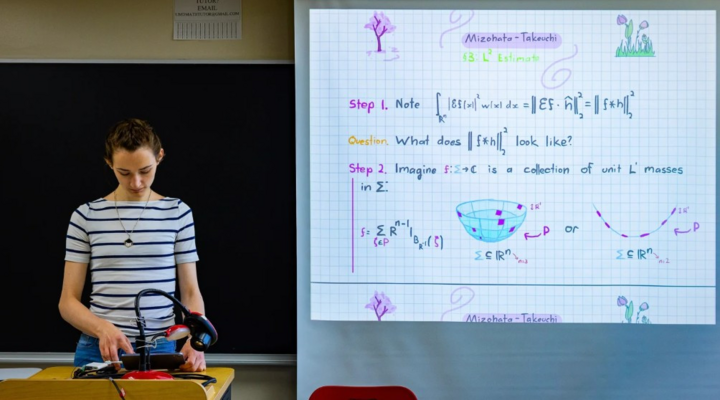
হান্না কায়রো বলেন যে তিনি রঙিন, সুন্দর টুকরো দিয়ে গণিত উপস্থাপন করতে উপভোগ করেন। (ছবি: কোয়ান্টা ম্যাগাজিন)

কিন্তু নিরুৎসাহিত হওয়ার পরিবর্তে, তিনি পড়া, চিন্তাভাবনা এবং পরীক্ষা-নিরীক্ষা চালিয়ে যান। অবশেষে, কায়রো বক্র পৃষ্ঠের কম্পাঙ্কের তরঙ্গ থেকে একটি অদ্ভুত ফাংশন তৈরি করে - ঠিক যেমনটি অনুমানের প্রয়োজন ছিল। স্বাভাবিকভাবে একে অপরকে বাতিল এবং প্রশস্ত করার পরিবর্তে, তরঙ্গগুলি তাদের শক্তি অনিয়মিত, প্রায় ফ্র্যাক্টাল-সদৃশ প্যাটার্নে ছড়িয়ে দেয় - যা অনুমানের দাবি অনুসারে ঘটতে পারে না।

"কায়রোর গবেষণাপত্র দেখায় যে আপাতদৃষ্টিতে স্পষ্ট এবং মার্জিত অনুমানগুলি এখনও অপ্রত্যাশিত উপায়ে ভেঙে যেতে পারে," গণিতবিদ ফার্নান্দো অলিভেরা বলেন। "কিন্তু এটি দেখার জন্য, আপনার সঠিক 'পরিধি' প্রয়োজন।"

গণিতবিদ অ্যান্থনি কার্বেরি বলেন: "আমি ছিলাম, 'বাহ!' এটি এমন একটি সমস্যা যা আমি গত ৪০ বছর ধরে ভালোবাসি। কায়রোর সমাধান কেবল আকর্ষণীয়ই নয় বরং অসাধারণ পরিশীলিততাও দেখায়। যখন আমি জানতে পারলাম যে লেখকের বয়স মাত্র ১৭ বছর, তখন আমি আরও অবাক হয়েছিলাম।"

এই আবিষ্কার কেবল কয়েক দশকের পুরনো একটি অনুমানকেই ভেঙে দেয় না, বরং সুরেলা বিশ্লেষণের ক্ষেত্রে অনেক সমস্যার নতুন পদ্ধতিও খুলে দেয়। "এখন থেকে, অনুরূপ যেকোনো সমস্যা, আমরা কায়রো-শৈলীর নির্মাণ দিয়ে যাচাই করার চেষ্টা করব," যোগ করেন গণিতবিদ অলিভেরা।

মিজোহাতা-তাকেউচি অনুমান প্রত্যাখ্যানের একটি বড় পরিণতিও হয়েছিল: স্টেইন অনুমান, যা আরও অনেক সমস্যার সমাধান করবে বলে আশা করা হয়েছিল, এখন পুনর্বিবেচনা করতে বাধ্য হয়েছিল। গণিতকে আবারও তার দিক পরিবর্তন করতে হয়েছিল।

স্নাতক ডিগ্রি ছেড়ে সরাসরি ডক্টরেটে যান

কোয়ান্টা ম্যাগাজিনের মতে, ফলাফল ঘোষণার পর, কায়রো স্নাতক স্তর বাদ দিয়ে সরাসরি তার ডক্টরেটে যাওয়ার সিদ্ধান্ত নেয়। তিনি যে ১০টি বিশ্ববিদ্যালয়ে আবেদন করেছিলেন, তার মধ্যে বেশিরভাগই তাকে প্রত্যাখ্যান করে কারণ কায়রোতে উচ্চ বিদ্যালয় বা বিশ্ববিদ্যালয়ের ডিগ্রি ছিল না। দুটি স্কুল প্রথমে সম্মত হয়েছিল কিন্তু পরে প্রশাসকরা তা বন্ধ করে দেয়।

শেষ পর্যন্ত, শুধুমাত্র মেরিল্যান্ড বিশ্ববিদ্যালয় এবং জনস হপকিন্স তাকে গ্রহণ করে। কায়রো মেরিল্যান্ডকে বেছে নেয়, যেখানে তিনি এই শরতে তার ডক্টরেট যাত্রা শুরু করবেন - তার প্রথম আনুষ্ঠানিক ডিগ্রি।

(সূত্র: ভিয়েতনামনেট)

লিঙ্ক: https://vietnamnet.vn/thieu-nu-17-tuoi-giai-ma-duoc-bi-an-toan-hoc-ton-tai-suot-40-nam-2432764.html

সূত্র: https://vtcnews.vn/thieu-nu-17-tuoi-giai-ma-duoc-bi-an-toan-hoc-ton-tai-suot-40-nam-ar960239.html