2025年ハノイ10年生入学試験の数学解答例

ハノイ市教育訓練局は、2025年の10年生入学試験の7科目のサンプル問題を発表しました。この7科目は、文学、数学、外国語、自然科学、歴史と地理、公民、情報技術です。

2025 年度ハノイ10 年生入学試験の例示的な数学試験 (スクリーンショット)。

数学の場合、試験の知識は 3 つの部分で構成されます。数字と代数は 4.5 ポイント、幾何学と測定は 4 ポイント、統計と確率は 1.5 ポイントです。

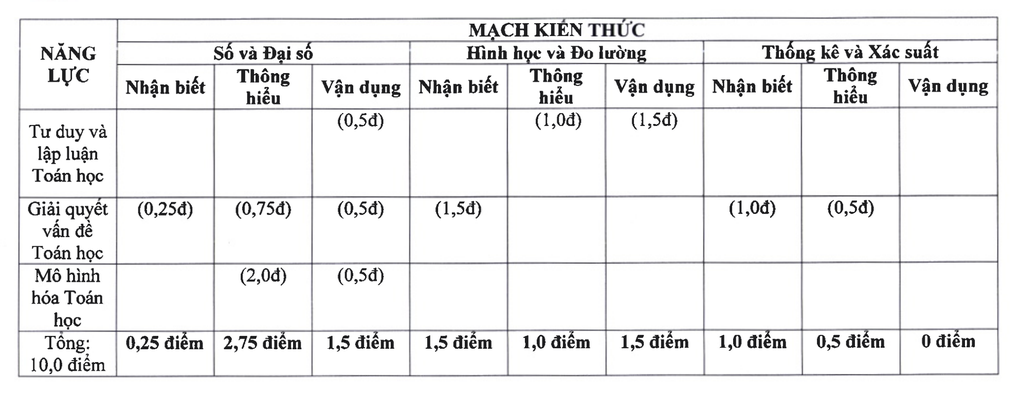
2025 年ハノイの 10 年生入学試験の数学の知識回路 (スクリーンショット)。

>> 2025年ハノイ公立10年生数学試験の詳細な解答例をtuyensinh247の専門部門の教師から見る

数学イラストテスト復習

Do Van Bao 先生によると、試験の一般的な構成は次のとおりです。

パート I: (1.5 ポイント) 統計と確率に関する質問が 2 つ含まれます。

- データ統計、グラフ

- 確率

パート II: (1.5 点) 前年度の試験の質問 I に類似した代数式に関する質問が 3 つ含まれています。

- 式の値を計算し、生徒の基礎スキルをテストします

- 表現を簡素化する

- 生徒を区別するための追加の質問

パート III: (2.5 ポイント) 連立方程式と二次方程式に関連する 3 つの質問が含まれます。

- 質問1、2: 連立方程式を立てて現実の問題を解く

- 問3 二次方程式

レッスンIV. 幾何学

- 空間幾何学

- 円に関する問題

レッスン V. 実用的な要因に関連する幾何学的極値に関する高度な問題。

合計スコア: 10 ポイント、代数、幾何学から実用的な応用まで、基礎知識と高度な知識のセクションに均等に配分されます。

知識コンテンツに関するコメント

代数セクション：式を使った計算、二次方程式、その応用といった基本的な内容が含まれています。このイラストテストの新たな特徴は、実生活の問題を題材にした問題が多く出題され、生徒が数学を通して人生の課題に取り組むことができる点です。

幾何学セクション：平面幾何学、円や内接四角形に関する問題、空間幾何学、幾何学の証明、そして実践における幾何学の応用といった、馴染みのある内容が含まれます。試験では、優れた空間思考力と、幾何学理論を実践的な問題に適用する能力が求められます。

統計と確率のセクション: 前年度の試験と比較して新しい内容で、レッスン I に登場し、生徒にグラフを分析して確率を計算することを要求します。これは実用的な内容であり、新しい教科書プログラムに頻繁に登場します。

難易度に関するコメント

初級・中級レベル：式の評価、二次方程式の解き方、確率の計算など、いずれも初級・中級レベルの問題です。これらの問題に解答するには、基礎をしっかりと理解している必要があります。

上級レベル：幾何学の証明、空間幾何学を含む実践的な問題、銀行の利子計算問題など、高度な論理的思考力と知識を実践に応用する能力が問われます。これらの問題は、平均的な学習能力を持つ生徒にとって、しばしば難解となるでしょう。

ハノイの模擬試験は、新しい一般教育プログラムに厳密に従うように設計されており、学生の知識とスキル、特にそれらを実践に応用する能力を総合的にテストすることに重点を置いています。

この試験は、従来の構成の 60 ～ 70% を維持していますが、内容と質問の作成方法が革新され、学生をより総合的に評価するのに役立ちます。

試験の難易度は中程度で、優秀な学生を選抜するために明確な差別化が図られています。

これまでの試験では、純粋な代数と幾何学の問題によって、優秀な生徒と平均的な生徒の差が明確に表れることが多かった。今回の模擬試験では実践的な要素が加わり、生徒は知識だけでなく、その知識を具体的な状況にどのように応用するかを理解することが求められるようになった。

今年の模擬試験の構成は、昨年度と比べて大幅に刷新されました。授業における知識内容の分類、問題形式のインターリービング、そして特に実践的な問題の増加が図られています。これは、生徒の知識の応用力と思考の統合力の測定に重点を置くという、新しい教育プログラムの方向性を反映しています。

試験で良い成績を取るには、9 年生は次のものが必要です。

サンプル試験と同じ構成と内容で 10 年生の入学試験に十分に備えるために、9 年生は次の手順に従う必要があります。

1. 基本を押さえる

代数: 9 年生のプログラムで以下の基礎知識を習得する必要があります:

1 次および 2 次方程式、解、および特性。

平面幾何学と立体幾何学に関連する公式、特に三角形、円、基本的な幾何学的形状に関連する定理。

方程式を立てて問題を解く

幾何学: 知識、円に関する定理、内接四辺形とその性質、相似三角形の証明、相似三角形の性質の適用など。

統計と確率: 頻度グラフ、頻度表、簡単な確率計算などの基本的な統計概念は試験に出題される可能性があるため、これらの分野に精通している必要があります。

2. 実際の数学の問題を解く練習をする

応用数学: 生徒は、実生活に関連する問題、方程式の設定による問題解決、連立方程式、生産および管理の問題、または空間幾何学に関連する問題を練習する必要があります。

知識を現実に応用する：体積や面積の測定と計算に関する問題を、実際の状況で練習します。これにより、生徒は数学を現実に応用する方法をより深く理解することができます。

3. 論理的思考力と分析力を鍛える

数学的証明：幾何学と代数の証明問題の練習を強化します。特に、平面幾何学や空間幾何学における要素間の関係性を証明する問題は、論理的思考力を向上させるために不可欠です。

問題を分析して解く：問題を解き始める前に、問題を分析し、各問題の要件を理解する練習をしましょう。これにより、混乱を避け、試験の正確性を高めることができます。

出典: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm