2025 में हनोई में 10वीं कक्षा की प्रवेश परीक्षा के लिए सुझाए गए गणित के उत्तर

हनोई शिक्षा और प्रशिक्षण विभाग ने 2025 में 10वीं कक्षा की प्रवेश परीक्षा के लिए 7 विषयों के नमूना प्रश्नों की घोषणा की है। इन 7 विषयों में साहित्य, गणित, विदेशी भाषाएं, प्राकृतिक विज्ञान, इतिहास और भूगोल, नागरिक शास्त्र और सूचना प्रौद्योगिकी शामिल हैं।

हनोई में 2025 स्कूल वर्ष में ग्रेड 10 प्रवेश परीक्षा के लिए उदाहरणात्मक गणित परीक्षा (स्क्रीनशॉट)।

गणित के लिए, परीक्षा के ज्ञान में 3 भाग होते हैं: संख्या और बीजगणित के लिए 4.5 अंक, ज्यामिति और माप के लिए 4 अंक, सांख्यिकी और संभाव्यता के लिए 1.5 अंक।

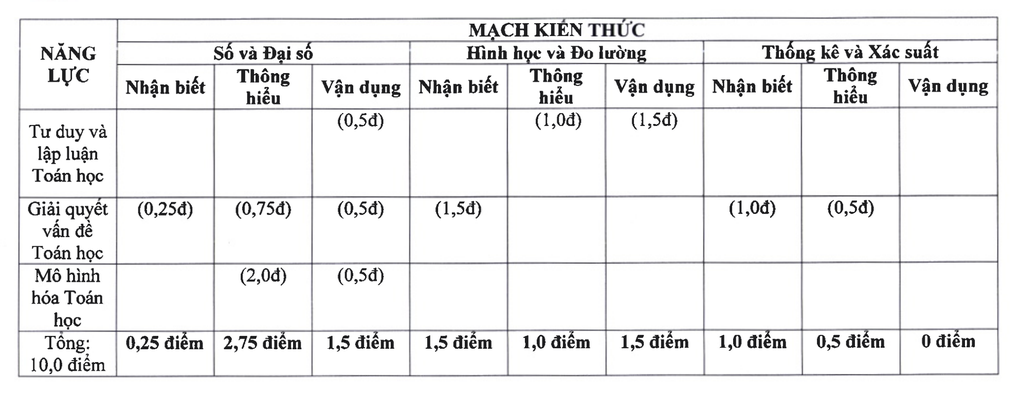
2025 में हनोई में 10वीं कक्षा की प्रवेश परीक्षा के लिए गणित ज्ञान सर्किट (स्क्रीनशॉट)।

>> 2025 में हनोई में सार्वजनिक ग्रेड 10 के लिए गणित परीक्षा के लिए व्यावसायिक विभाग tuyensinh247 के शिक्षकों से विस्तृत सुझाए गए उत्तर यहां देखें

गणित चित्रण परीक्षण की समीक्षा

शिक्षक डो वान बाओ के अनुसार, परीक्षा की सामान्य संरचना इस प्रकार है:

भाग I: (1.5 अंक) इसमें सांख्यिकी और संभाव्यता पर 2 प्रश्न शामिल हैं।

- डेटा सांख्यिकी, चार्ट

- संभावना

भाग II: (1.5 अंक) इसमें बीजीय व्यंजकों पर 3 प्रश्न सम्मिलित हैं, जो पिछले वर्षों की परीक्षाओं के प्रश्न I के समान हैं।

- अभिव्यक्ति मूल्यों की गणना करें, छात्रों के बुनियादी कौशल का परीक्षण करें

- अभिव्यक्ति को सरल बनाएं

- छात्रों में अंतर करने के लिए अतिरिक्त प्रश्न

पाठ III: (2.5 अंक) इसमें समीकरणों की प्रणालियों और द्विघात समीकरणों से संबंधित 3 प्रश्न शामिल हैं।

- वाक्य 1,2: समीकरणों की एक प्रणाली स्थापित करके वास्तविक जीवन की समस्याओं को हल करें, समीकरण स्थापित करें

- प्रश्न 3 द्विघात समीकरण

पाठ IV. ज्यामिति

- स्थानिक ज्यामिति

- वृत्तों से संबंधित समस्याएँ

पाठ V. वास्तविक दुनिया के कारकों से संबंधित ज्यामितीय चरम सीमाओं पर उन्नत समस्याएं।

कुल अंक: 10 अंक, बीजगणित, ज्यामिति से लेकर व्यावहारिक अनुप्रयोगों तक, बुनियादी और उन्नत ज्ञान वर्गों के बीच समान रूप से वितरित।

ज्ञान सामग्री पर टिप्पणियाँ

बीजगणित अनुभाग: इसमें व्यंजकों के साथ गणनाएँ, द्विघात समीकरण और अनुप्रयोग जैसी बुनियादी सामग्री शामिल है। नमूना परीक्षा की नई विशेषता यह है कि इसमें कई प्रश्न वास्तविक जीवन की समस्याओं का उपयोग करते हैं, जिससे छात्रों को गणित के माध्यम से जीवन की समस्याओं का समाधान करने में मदद मिलती है।

ज्यामिति अनुभाग: इसमें समतल ज्यामिति, वृत्तों और उत्कीर्ण चतुर्भुजों से संबंधित समस्याएँ, स्थानिक ज्यामिति, ज्यामितीय प्रमाण और व्यवहारिक ज्यामितीय अनुप्रयोग जैसी परिचित विषय-वस्तु शामिल है। इस परीक्षा के लिए छात्रों में अच्छी स्थानिक सोच और ज्यामितीय सिद्धांत को व्यावहारिक समस्याओं पर लागू करने की क्षमता होना आवश्यक है।

सांख्यिकी और संभाव्यता अनुभाग: पिछले वर्ष की परीक्षाओं की तुलना में नई सामग्री है, जो पाठ I में दिखाई देती है, जिसमें छात्रों को ग्राफ का विश्लेषण करने और संभाव्यता की गणना करने की आवश्यकता होती है, जो व्यावहारिक अनुप्रयोग से संबंधित है और अक्सर नई पाठ्यपुस्तक कार्यक्रमों में दिखाई देती है।

कठिनाई पर टिप्पणियाँ

बेसिक और इंटरमीडिएट स्तर: व्यंजकों का मूल्यांकन, द्विघात समीकरणों को हल करना और प्रायिकता की गणना से संबंधित प्रश्न बेसिक और इंटरमीडिएट स्तर के हैं। इन प्रश्नों को हल करने के लिए छात्रों को केवल मूल बातों पर अच्छी पकड़ होनी चाहिए।

उन्नत स्तर: ज्यामितीय प्रमाणों, स्थानिक ज्यामिति से संबंधित व्यावहारिक समस्याओं और बैंक ब्याज गणनाओं से संबंधित प्रश्नों के लिए छात्रों में अच्छी तार्किक सोच और ज्ञान को व्यवहार में लागू करने की क्षमता आवश्यक है। ये प्रश्न अक्सर औसत सीखने की क्षमता वाले छात्रों के लिए चुनौतीपूर्ण होंगे।

हनोई की नमूना परीक्षा नए सामान्य शिक्षा कार्यक्रम का बारीकी से अनुसरण करने के लिए तैयार की गई है, जो छात्रों के ज्ञान और कौशल, विशेष रूप से उन्हें व्यवहार में लागू करने की उनकी क्षमता का व्यापक परीक्षण करने पर केंद्रित है।

परीक्षा में 60-70% पारंपरिक संरचना बरकरार रखी गई है, लेकिन विषय-वस्तु और प्रश्न-निर्माण विधियों में नवीनताएं हैं, जिससे छात्रों का अधिक व्यापक मूल्यांकन करने में मदद मिलती है।

परीक्षा की कठिनाई मध्यम है, तथा अच्छे छात्रों का चयन करने के लिए स्पष्ट विभेदन किया गया है।

पिछले वर्षों में, परीक्षा में अक्सर शुद्ध बीजगणित और ज्यामिति के प्रश्नों के माध्यम से अच्छे और औसत छात्रों के बीच स्पष्ट अंतर किया जाता था। नमूना परीक्षा में व्यावहारिक तत्व जोड़े गए हैं, जिससे छात्रों को न केवल ज्ञान होना आवश्यक है, बल्कि यह भी समझना होगा कि उस ज्ञान को विशिष्ट परिस्थितियों में कैसे लागू किया जाए।

इस वर्ष उदाहरणात्मक परीक्षा की संरचना में पिछले वर्षों की तुलना में काफ़ी नवीनता लाई गई है, जिसमें पाठों में ज्ञान की सामग्री का वर्गीकरण, प्रश्नों के प्रकारों का अंतर्संबंध और विशेष रूप से व्यावहारिक समस्याओं में वृद्धि शामिल है। यह नए शिक्षा कार्यक्रम की दिशा को दर्शाता है, जो छात्रों की ज्ञान को लागू करने और सोच को संश्लेषित करने की क्षमता के परीक्षण पर अधिक ध्यान केंद्रित करता है।

परीक्षा में अच्छा प्रदर्शन करने के लिए 9वीं कक्षा के छात्रों को चाहिए:

नमूना परीक्षा के समान संरचना और विषय-वस्तु के साथ 10वीं कक्षा की प्रवेश परीक्षा की अच्छी तैयारी के लिए, 9वीं कक्षा के छात्रों को इन चरणों का पालन करना होगा:

1. मूल बातें समझें

बीजगणित: 9वीं कक्षा के कार्यक्रम में बुनियादी ज्ञान में महारत हासिल करने की आवश्यकता है, जिसमें शामिल हैं:

प्रथम एवं द्वितीय डिग्री समीकरण, समाधान एवं गुणधर्म।

समतल और ठोस ज्यामिति से संबंधित सूत्र, विशेष रूप से त्रिभुज, वृत्त और मूल ज्यामितीय आकृतियों से संबंधित प्रमेय।

समीकरण स्थापित करके समस्याओं को हल करें

ज्यामिति: ज्ञान, वृत्तों, उत्कीर्ण चतुर्भुजों और गुणों के बारे में प्रमेय, समरूप त्रिभुजों को सिद्ध करना और समरूप त्रिभुजों के गुणों को लागू करना,...

सांख्यिकी और प्रायिकता: हिस्टोग्राम, आवृत्ति सारणी, सरल प्रायिकता गणना जैसी बुनियादी सांख्यिकीय अवधारणाओं से परिचित होना आवश्यक है, क्योंकि ये ऐसे खंड हैं जो परीक्षा में आ सकते हैं।

2. वास्तविक गणित की समस्याओं को हल करने का अभ्यास करें

अनुप्रयुक्त गणित: छात्रों को वास्तविक जीवन से संबंधित समस्याओं, समीकरण स्थापित करके समस्या समाधान, समीकरणों की प्रणाली, उत्पादन और प्रबंधन समस्याओं, या स्थानिक ज्यामिति से संबंधित समस्याओं के साथ अभ्यास करने की आवश्यकता है।

ज्ञान को वास्तविकता में लागू करना: व्यावहारिक परिस्थितियों में आयतन और क्षेत्रफल मापने और गणना करने से संबंधित समस्याओं का अभ्यास करें। इससे छात्रों को यह समझने में मदद मिलती है कि गणित को जीवन में कैसे लागू किया जाए।

3. तार्किक सोच और विश्लेषणात्मक कौशल का अभ्यास करें

गणितीय प्रमाण: ज्यामितीय और बीजगणितीय प्रमाण समस्याओं में अभ्यास को मज़बूत करें। विशेष रूप से, समतल या स्थानिक ज्यामिति में तत्वों के बीच संबंधों के प्रमाण की आवश्यकता वाली समस्याएँ तार्किक सोच को बेहतर बनाने के लिए आवश्यक हैं।

समस्याओं का विश्लेषण और समाधान करें: प्रश्नों का विश्लेषण करने का अभ्यास करें और उन्हें हल करने से पहले प्रत्येक प्रश्न की आवश्यकताओं को समझें। इससे भ्रम से बचने और परीक्षा प्रक्रिया में सटीकता बढ़ाने में मदद मिलती है।

स्रोत: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm