Επιστήμονες βρίσκουν λύση σε ένα κλασικό γεωμετρικό πρόβλημα που διήρκεσε περισσότερο από έναν αιώνα

Εικονογράφηση για γεωμετρικό πρόβλημα.

Σύμφωνα με την εφημερίδα South China Morning Post, ο μαθηματικός Hong Wang – ο οποίος είναι επί του παρόντος αναπληρωτής καθηγητής στο Ινστιτούτο Μαθηματικών Επιστημών Courant του Πανεπιστημίου της Νέας Υόρκης (ΗΠΑ) – και ο συνάδελφός του Joshua Zahl (Πανεπιστήμιο της Βρετανικής Κολομβίας, Καναδάς) μόλις έλυσαν ένα από τα πιο δύσκολα προβλήματα γεωμετρίας του 20ού - 21ου αιώνα: την Εικασία Kakeya στον τρισδιάστατο χώρο.

Ο Χονγκ Γουάνγκ γεννήθηκε στην πόλη Γκουιλίν (Κίνα), σπούδασε στο Πανεπιστήμιο του Πεκίνου προτού διδάξει και ασχοληθεί με την έρευνα στις ΗΠΑ.

Το πρόβλημα ξεκίνησε το 1917, όταν ο Ιάπωνας μαθηματικός Sōichi Kakeya έθεσε το ερώτημα: «Ποια είναι η μικρότερη επιφάνεια που απαιτείται για να περιστραφεί μια βελόνα κατά 180 μοίρες;» Αυτός ο ελάχιστος χώρος ονομάζεται «σύνολο Kakeya».

Σε δισδιάστατο χώρο, η περιστροφή της βελόνας για να σχηματίσει έναν κύκλο είναι εύκολο να απεικονιστεί, αλλά αν η περιστροφή είναι πιο ευέλικτη, όπως το κούνημα της βελόνας κατά την περιστροφή, η περιοχή που σαρώνει η βελόνα μπορεί να είναι ακόμη μικρότερη.

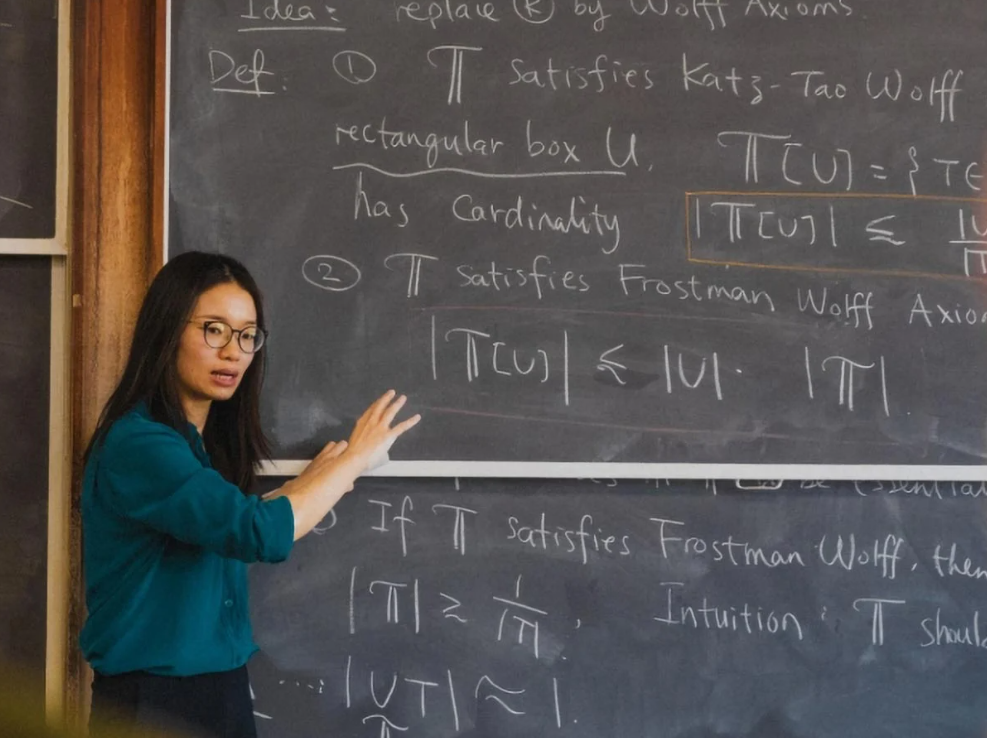
Επιστήμονες βρίσκουν λύση σε γεωμετρικό πρόβλημα που διήρκεσε περισσότερο από έναν αιώνα.

Η μετακίνηση του προβλήματος σε τρεις διαστάσεις το καθιστά πολύ πιο περίπλοκο. Η εικασία του Kakeya αναφέρει ότι αν θέλετε να περιστρέψετε τη βελόνα προς όλες τις κατευθύνσεις, ο χώρος που απαιτείται πρέπει να είναι αρκετά μεγάλος και στις τρεις διαστάσεις - δεν μπορείτε να τη στριμώξετε σε ένα σημείο που είναι πολύ μικρό ή πολύ λεπτό.

Στην εργασία τους, που δημοσιεύτηκε στην πλατφόρμα arXiv, οι Wang και Zahl αποδεικνύουν ότι, στον τρισδιάστατο χώρο, η περιοχή στην οποία περιστρέφεται η βελόνα δεν χρειάζεται να έχει σαφές σχήμα, αλλά πρέπει να είναι αρκετά μεγάλη και στις τρεις διαστάσεις. Χάρη σε αυτό, έλυσαν αυτό το πρόβλημα - που θεωρείται μια πολύ σημαντική ανακάλυψη στα μαθηματικά σήμερα.

Ο καθηγητής Τέρενς Τάο – ένας από τους κορυφαίους μαθηματικούς στον κόσμο , χαρακτήρισε αυτό το έργο «εντυπωσιακή πρόοδο». Οι ειδικοί δήλωσαν επίσης ότι το έργο όχι μόνο διεύρυνε την κατανόηση της γεωμετρίας, αλλά θα μπορούσε επίσης να επηρεάσει πολλούς τομείς όπως η επεξεργασία εικόνας, οι ασύρματες επικοινωνίες, η επιστήμη των υπολογιστών και η κρυπτογραφία – όπου η κατανόηση των κινήσεων και των αλληλεπιδράσεων στο διάστημα είναι εξαιρετικά σημαντική.

«Δεν είναι υπερβολή, αλλά πρόκειται για μια σπάνια λύση που περιμέναμε εκατοντάδες χρόνια», δήλωσε ο καθηγητής Μαθηματικών Νετς Κατζ, ο οποίος διδάσκει στο Πανεπιστήμιο Ράις (ΗΠΑ).

Σύμφωνα με τον καθηγητή Guth Larry, λέκτορα στο Τεχνολογικό Ινστιτούτο της Μασαχουσέτης (ΗΠΑ), η υπόθεση Kakeya αποτελεί το θεμέλιο ενός «πύργου» μεγαλύτερων υποθέσεων στον τομέα της γεωμετρίας. Η επίλυση αυτής της υπόθεσης θα βοηθήσει τα υψηλότερα επίπεδα του πύργου της γνώσης να έχουν την ευκαιρία να προσεγγιστούν και να κατακτηθούν.

«Παλιότερα νόμιζα ότι επρόκειτο για ένα απλό, βασικό πρόβλημα γεωμετρίας, αλλά στην πραγματικότητα, αυτό το πρόβλημα είναι πολύ δύσκολο. Αυτό το πρόβλημα έχει επιλυθεί από πολλά μεγάλα ονόματα στον τομέα των μαθηματικών, αλλά τα περισσότερα από αυτά πέτυχαν μόνο μικρά αποτελέσματα, δεν ήταν συστηματικά και δεν μπορούσαν να θεωρηθούν ως ολοκληρωμένη λύση», μοιράστηκε ο καθηγητής Guth Larry.

Phuong Anh (Πηγή: Science Daily, SCMP)

Πηγή: https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-hinh-hoc-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html