एआई युग में गणित की परीक्षा कैसे बदलें?

एआई अनुसंधान विशेषज्ञों का मानना ​​है कि गणित की परीक्षा में बदलाव की आवश्यकता है, परीक्षा में निबंध प्रश्न जोड़ना कृत्रिम बुद्धिमत्ता विस्फोट के युग में सही कदम होगा।

हाल ही में, गणित की परीक्षा और अंकों के वितरण को लेकर कई विशेषज्ञों की राय अलग-अलग रही है। ब्रिटिश यूनिवर्सिटी वियतनाम (BUV) के कंप्यूटर विज्ञान एवं प्रौद्योगिकी संकाय में कृत्रिम बुद्धिमत्ता (AI) के शोधकर्ता और व्याख्याता डॉ. डांग क्वांग विन्ह ने भी थान निएन अखबार के साथ AI के नज़रिए से एक दिलचस्प सुझाव साझा किया है। उन्होंने उम्मीद जताई है कि शिक्षा एवं प्रशिक्षण मंत्रालय निकट भविष्य में गणित की परीक्षा में बदलाव करेगा।

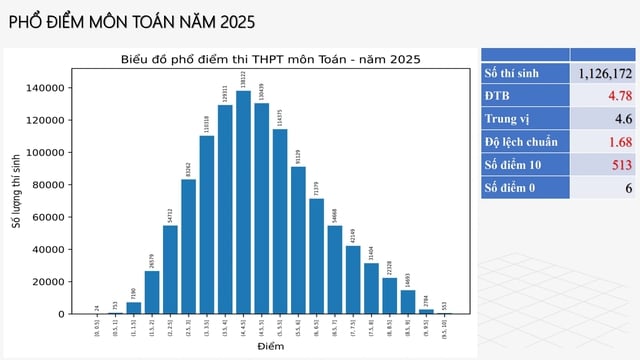
2025 में गणित स्कोर वितरण सामान्य वितरण के करीब पहुंच जाएगा

हालाँकि, डॉ. विन्ह ने इस वर्ष की गणित परीक्षा के अंक वितरण पर भी सकारात्मक टिप्पणी की। हाल के वर्षों में गणित के अंक वितरण की तुलना में, हाई स्कूल स्नातक परीक्षा की गणित परीक्षा का अंक वितरण सामान्य वितरण के सबसे करीब है। इससे पता चलता है कि इस वर्ष की गणित परीक्षा में उच्च विभेदन है।

हालाँकि अंक वितरण पिछले वर्ष की तुलना में कम प्रतीत होता है, इस वर्ष का अंक वितरण सांख्यिकी में सामान्य वितरण की अवधारणा के अधिक निकट है। सैद्धांतिक रूप से, हम एक मानकीकृत परीक्षा से यही अपेक्षा कर सकते हैं, खासकर जब इसे हाई स्कूल परीक्षा में बैठने वाले उम्मीदवारों की संख्या जैसे बड़े डेटा सेट पर लागू किया जाए। ऐसे मामलों में, आदर्श अंक वितरण सामान्य वितरण के निकट होना चाहिए। इसलिए, यह अनुमान लगाया जा सकता है कि इस वर्ष का अंक वितरण उचित है।

कम अंक वितरण वास्तव में शिक्षा के लिए एक सकारात्मक संकेत है। यदि परीक्षा बहुत आसान है और कई उम्मीदवारों को पूरे अंक मिलते हैं, तो परीक्षा वास्तविक क्षमताओं को वर्गीकृत और मूल्यांकन करने का अपना कार्य खो देगी।

डॉ. विन्ह ने कहा: "हम सभी समझते हैं कि अंक केवल सापेक्ष क्षमता को दर्शाते हैं, लेकिन एक स्पष्ट अंतर, जैसे कि 8 और 3 के बीच, अभी भी तैयारी और सीखने की मानसिकता में अंतर को दर्शाता है। इसके अलावा, यदि बहुत से छात्रों को पूर्ण अंक मिलते हैं, तो यह भी दर्शाता है कि परीक्षा उनकी पूरी क्षमता का उपयोग करने के लिए पर्याप्त कठिन नहीं है, यह दर्शाता है कि ऐसे छात्र हैं जो उच्च स्तर, 11-12 या 15 अंक प्राप्त कर सकते हैं, यदि ग्रेडिंग स्केल अनुमति देता है।

इसलिए, उच्च अंकों पर केंद्रित न होकर, समान रूप से वितरित अंकों का स्पेक्ट्रम हमें उम्मीदवारों को बेहतर ढंग से वर्गीकृत करने और उनके लिए अपनी अधिकतम क्षमता प्रदर्शित करने हेतु परिस्थितियाँ बनाने में मदद करता है। यही इस वर्ष की गणित परीक्षा और अंकों के स्पेक्ट्रम का सकारात्मक पहलू है।"

ऐसा न पूछें कि अभ्यर्थियों को केवल उत्तर चुनना पड़े।

हालांकि, डॉ. विन्ह के अनुसार, एआई के नजरिए से, वर्तमान हाई स्कूल स्नातक परीक्षा की तरह पूरी तरह से बहुविकल्पीय गणित प्रश्न गणित शिक्षा के लक्ष्य के लिए उपयुक्त नहीं हैं।

हाल के वर्षों में, कई लोग इस बात से चिंतित रहे हैं कि एआई बहुत जल्दी उत्तर तो दे सकता है, लेकिन यह स्पष्ट नहीं कर सकता कि वह ऐसा क्यों सोचता है। यह एआई को उन क्षेत्रों में अविश्वसनीय बनाता है जहाँ कठोर तर्क की आवश्यकता होती है। इसलिए, वर्तमान विकास दिशा एआई में तर्क क्षमताओं को एकीकृत करने की है, ताकि यह न केवल सही परिणाम दे सके, बल्कि निष्कर्ष तक पहुँचने की प्रक्रिया को भी स्पष्ट कर सके।

और यही बात तर्क को इतना अनूठा मानवीय लाभ बनाती है कि एआई इसे प्राप्त करने के लिए काम कर रहा है।

"इसलिए, हमारे पास उस लाभ को छोड़ने का कोई कारण नहीं है। इसके विपरीत, शिक्षा को तर्क क्षमता को प्रोत्साहित करने और बढ़ावा देने की आवश्यकता है, विशेष रूप से निबंध परीक्षाओं के माध्यम से," डॉ. विन्ह ने कहा।

डॉ. विन्ह के अनुसार, गणित के इतिहास में हमने देखा है कि तर्क प्रक्रिया अक्सर अंतिम परिणाम से ज़्यादा मूल्यवान साबित होती है। केवल उत्तर की चिंता करना और तर्क को नज़रअंदाज़ करना गणितीय चिंतन की मूल भावना के विपरीत है।

विकास की वर्तमान दर को देखते हुए, एआई निश्चित रूप से परिणाम देने की क्षमता में मनुष्यों से आगे निकल जाएगा, खासकर विशुद्ध रूप से कम्प्यूटेशनल समस्याओं या ऐतिहासिक डेटा पुनर्प्राप्ति के मामले में। लेकिन तार्किक चिंतन प्रक्रियाओं की व्याख्या और प्रस्तुति में, कम से कम वर्तमान समय में, एआई मनुष्यों की जगह नहीं ले सकता।

डॉ. विन्ह ने कहा: "मैं छात्रों की तर्क करने और स्पष्ट रूप से सोचने की क्षमता का आकलन करने के लिए निबंध-आधारित परीक्षाओं के निर्माण का पूर्ण समर्थन करता हूँ। यही दृष्टिकोण हम बीयूवी में भी अपनाते हैं।"

कई स्कूली परीक्षाओं में, यहाँ तक कि कंप्यूटर विज्ञान एवं प्रौद्योगिकी विभाग में भी, जो कि साधारण गणनाओं पर केंद्रित क्षेत्र है, छात्रों से न केवल उत्तर देने की अपेक्षा की जाती है, बल्कि उसे लिखित रूप में या कक्षा में प्रस्तुतियों के माध्यम से समझाने की भी अपेक्षा की जाती है। किसी से यह नहीं पूछा जाता कि 1 + 1 कितना होता है और फिर बस 2 लिख दिया जाता है।

स्रोत: https://thanhnien.vn/thay-doi-de-thi-toan-the-nao-trong-thoi-dai-ai-185250719210628563.htm