직사각형의 둘레를 계산하는 공식은 무엇입니까?

수학 3 교과서에 따르면 직사각형의 둘레를 계산하려면 길이와 너비를 더한 다음 2를 곱합니다.

빠른 보기:

• 직사각형의 정의
• 직사각형의 속성
• 직사각형을 인식하는 표지판
• 직사각형의 둘레를 계산하는 공식
• 직사각형과 정사각형을 비교해보세요

직사각형의 정의

카이트북, 수학 3, 1권에서는 직사각형을 4개의 직각, 2개의 긴 변의 길이가 같고 2개의 짧은 변의 길이가 같은 도형으로 정의합니다.

직사각형의 속성

직사각형은 이등변 사다리꼴과 평행사변형의 모든 속성을 가지고 있습니다. 예를 들어,

- 마주보는 변의 쌍은 항상 평행하고 크기가 같습니다.

- 각도는 같고 90도입니다.

- 직사각형은 대각선과 변의 중점이 대칭입니다.

직사각형을 인식하는 표지판

- 세 개의 직각을 가진 사각형은 직사각형입니다.

- 한 각이 직각인 이등변 사다리꼴은 직사각형입니다.

- 한 각이 직각인 평행사변형은 직사각형입니다.

- 두 대각선의 길이가 같은 면은 직사각형입니다.

직사각형의 둘레를 계산하는 공식

수학 3 교과서에 따르면 직사각형의 둘레를 계산하려면 길이와 너비(측정 단위는 동일)를 더한 다음 2를 곱합니다.

P = (a+b) x 2

거기에

P는 직사각형의 둘레입니다.

a는 직사각형의 길이입니다.

b는 사각형의 너비입니다.

예를 들어: 길이가 6cm, 너비가 4cm인 직사각형의 둘레를 계산해 보세요.

답변: 직사각형의 둘레는 P = (6+4) x 2 = 20(cm)입니다.

직사각형과 정사각형을 비교해보세요

기준	구형	정사각형
가장자리	4변 중 마주보는 변 2쌍이 같다	4면, 4면 모두 동일하다
모서리	4개의 직각	4개의 직각
대각선	두 대각선은 서로 같고, 중점에서 교차하지만 수직이 아닙니다.	두 대각선은 서로 같고, 중점에서 만나며 서로 수직입니다.
둘레 계산 공식	P = (a+b) x 2	P = 4a
면적 계산 공식	S = axb	에스 = 아2

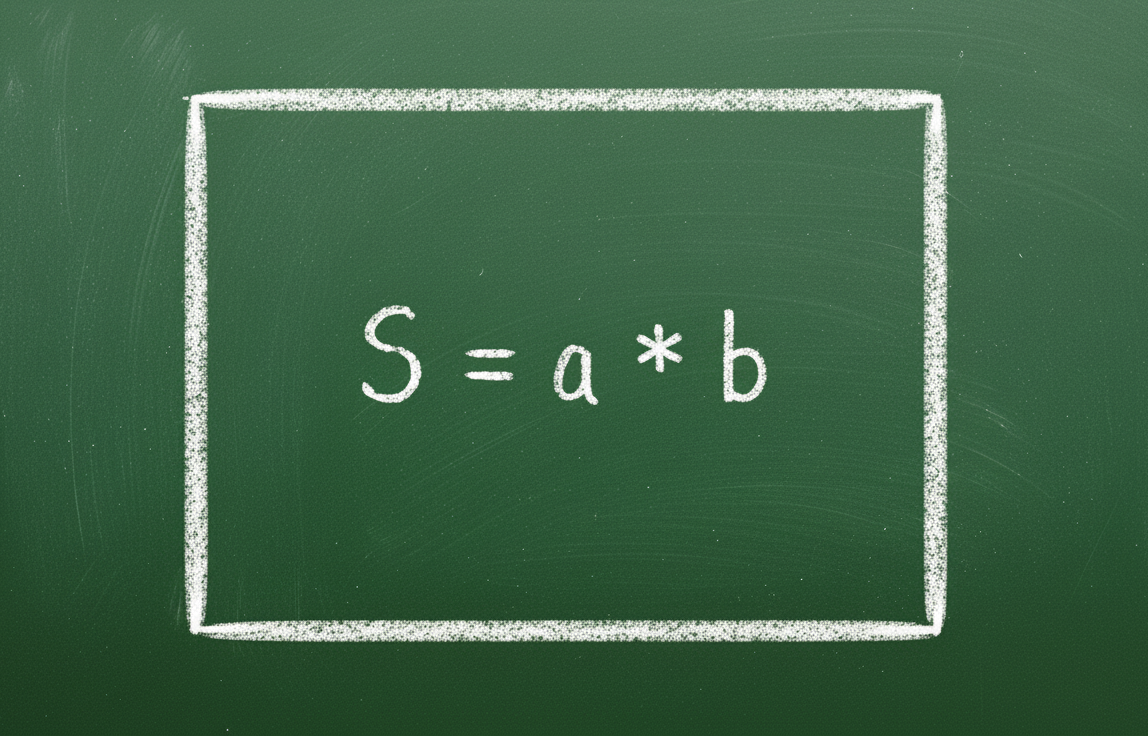
직사각형의 넓이를 구하는 공식 직사각형의 넓이를 구하는 방법은 길이와 너비를 곱하는 것 외에도, 한 변의 길이를 알고 대각선이나 둘레를 더하여 구할 수도 있습니다.

출처: https://vietnamnet.vn/cong-thuc-tinh-chu-vi-hinh-chu-nhat-la-gi-2452851.html