«Проблема с кипящей водой» на экзамене в 10-м классе вызвала споры

Хошимин: Задача о кипении воды на экзамене по математике в 10-м классе вызвала споры, поскольку ее посчитали нелогичной с точки зрения реальности и неверной с точки зрения знаний физики.

6 и 7 июня почти 96 000 кандидатов сдавали экзамены по литературе, иностранному языку и математике, чтобы поступить в 10-й класс государственных школ Хошимина. По словам учителей, экзамен по математике имел ту же структуру и сложность, что и в прошлом году. Экзамен состоял из 5 практических заданий (с третьего по седьмой вопрос).

После окончания экзамена г-н Май Ван Так, преподаватель физики в Высшей школе естественных наук Ханойского национального университета, сказал, что вопрос 5 на экзамене по математике для 10-го класса города Хошимин представлял собой правило, которого не существует в реальности и которое по своей природе неверно.

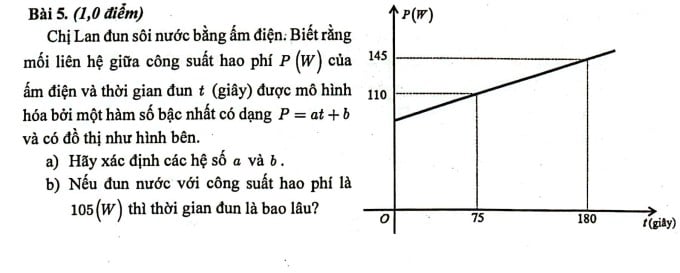
Вопрос 5 на экзамене по математике для поступления в 10-й класс государственной школы в городе Хошимин.

В частности, процесс преобразования энергии при кипячении воды рассчитывается с момента включения переключателя (при t = 0); электрическая энергия преобразуется в тепловую энергию, нагревая нагревательный провод (если чайник использует нагревательный провод). Нагревательный провод имеет более высокую температуру, чем вода в чайнике, и передает тепло воде, вода передает тепло чайнику, и требуется некоторое время, чтобы тепло было потеряно в окружающую среду. Мощность потери тепла в окружающую среду зависит главным образом от площади контакта чайника с окружающей средой и разницы температур между температурой чайника и окружающей средой (мощность потери также зависит от уровня циркуляции воздуха или ветра в месте нагрева). Когда мощность потери тепла в окружающую среду чайника станет равна мощности, получаемой нагревательным проводом, температура воды больше не будет повышаться.

Учитель Тук привёл пример нагревательного элемента мощностью 1000 Вт. Если вскипятить воду в двухлитровом чайнике, вода закипит, но если этот нагревательный элемент будет нагревать большой аквариум, то вода сможет нагреться только с 10 до 30 градусов Цельсия, после чего температура больше не повысится. В этот момент потери мощности постоянны и равны потребляемой мощности нагревательного элемента чайника. Таким образом, в вопросе 5 потери мощности определяются по правилу P = at + b, то есть t = 0, что соответствует потерям мощности 85 Вт, и эти потери постоянно растут, что неверно. Учитель также считает неверным вопрос: «Если вода кипятится с потерями мощности 105 Вт, сколько времени потребуется, чтобы она закипела?». Если предположить, что существует нелогичное правило, как у автора, то нужно спросить: «Рассчитать время кипения, пока потери мощности не достигнут 105 Вт».

С этими аргументами г-н Тук предложил Департаменту образования и профессиональной подготовки города Хошимин скорректировать ответ на вопрос 5, чтобы обеспечить равноправие кандидатов. Этот учитель считает, что ученики, хорошо владеющие физикой, могут не справиться с вопросом 5, если данные в задании слишком необычны.

Между тем, г-н Лам Ву Конг Чинь, учитель математики в средней школе Нгуен Ду в Хошимине, заявил, что с точки зрения знания физики и действительности данные в вопросе 5 не являются разумными и логичными. Однако, если вопрос представляет собой просто обзор, синтез и формулу прогнозирования, а не точную физическую формулу, он всё равно приемлем.

Г-н Чинь привёл пример оценки роста населения. По его словам, для этой задачи не существует абсолютно точной формулы, однако эксперты всё же применяют её, основываясь на определённых правилах и фактах, для прогнозирования и оценки будущей численности населения.

«Если студенты применяют математические знания, они всё равно смогут решить задачу нормально. Эта ошибка не влияет на результаты экзамена кандидатов», — сказал г-н Чинь.

Г-жа Нгуен Тьен Туй, учитель математики в средней школе Ха Хюй Тап в городе Хошимин, отметила, что вопрос 5 относится к задаче на функцию первой степени. В задаче дана формула функции первой степени с понятными формулами для каждой величины и единицы измерения, а также графические иллюстрации, чтобы учащиеся могли решить её обычным способом.

Кандидаты общаются после экзамена по математике, утро 7 июня. Фото: Ле Нгуен — Кандидаты общаются после экзамена по математике, утро 7 июня. Фото *: Ле Нгуен*

9 июня Департамент образования и профессиональной подготовки города Хошимин объявил, что вопрос 5 вступительного экзамена по математике для 10-го класса затрагивает тему, связанную с реальным явлением процесса закипания воды в электрическом чайнике. Этот процесс исследования представляет собой лишь краткий этап процесса закипания воды, и время начала исследования (t = 0) не совпадает с началом процесса закипания воды.

Полученные в ходе этого процесса данные математически описываются в виде рисунка и функции, изученной учащимися в программе. Таким образом, обладая математическими знаниями и навыками (функция первой степени, график функции первой степени, точки на графике, система уравнений первой степени с двумя неизвестными, вычислительные навыки), учащиеся могут решить поставленные в задаче задачи.

«В случаях, когда решения учащихся отличаются от инструкций по выставлению оценок, но являются разумными, они будут рассмотрены и оценены», — сообщили в Департаменте информации.

В прошлом году около 45% кандидатов, сдававших вступительный экзамен в 10-й класс в Хошимине, набрали ниже среднего балла по математике.

В этом году в Хошимине около 96 000 учащихся сдают вступительные экзамены в 10-й класс. Общая квота для 108 государственных средних школ города составляет 77 300 человек, а процент поступления составляет около 80%. Министерство образования и профессиональной подготовки сообщило, что результаты экзамена будут объявлены 20 июня.

Ле Нгуен

Ссылка на источник