90년대생 여성 준교수, 100년 가까이 지속된 '극도로 어려운' 문제 해결에 기여

세기의 문제

스미소니언 매거진에 따르면, 1917년 일본의 수학자 소이치 카케야가 다음과 같은 문제를 제기했습니다. 바늘을 360도 회전시키면서 쓸어지는 면적을 최소화하는 방법은 무엇일까요?

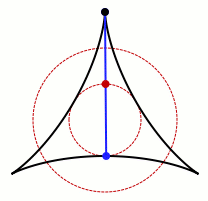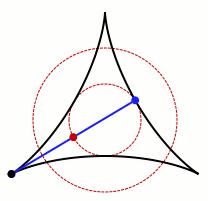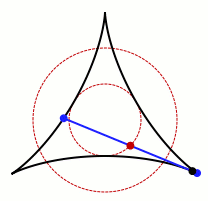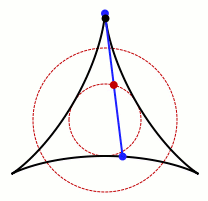
중심을 중심으로 회전시키면 바늘 끝이 원을 이루지만, 회전하면서 바늘을 살짝 흔드는 등 움직임을 조절하면 원의 면적을 더 줄일 수 있습니다. 여기서 문제는 선들이 어떻게 교차할 수 있는지에 대한 질문으로 확장됩니다. 겉보기에 간단해 보이지만 수학의 여러 분야에 깊은 영향을 미치는 질문입니다.

2차원에서는 카케야 추측이 증명되었지만, 3차원으로 옮기자 문제는 엄청나게 복잡해졌고 수십 년 동안 해결되지 않은 채 남았습니다.

부옹 홍4.jpg — 미국 뉴욕대학교 Vuong Hong 박사. 사진: *뉴욕대학교 팬페이지*

최근 두 수학자, 브엉 홍(뉴욕대학교, 미국)과 조슈아 잘(브리티시컬럼비아대학교, 캐나다)은 3차원 공간에서 카케야 추측을 증명하는 127페이지 분량의 논문을 발표했습니다. 아직 공식적으로 검토되지는 않았지만, 이 논문은 수학계에서 획기적인 발견으로 평가받고 있습니다.

2006년 필즈 메달 수상자인 호주계 미국인이자 중국 출신의 수학 천재 테렌스 타오는 이 연구에 곧바로 주목했습니다. 타오는 소셜 네트워크 마스토돈에 "기하학적 측도론에서 가장 인기 있는 미해결 문제 중 하나인 카케야 집합 추측이 왕훙과 조슈아 잘에 의해 (3차원에서) 증명되었다는 소식을 전하게 되어 기쁩니다."라고 글을 남겼습니다.

이 교수는 왕홍과 찰의 127페이지 분량의 논문이 출판된 지 하루 만에 자신의 개인 블로그에 이를 요약하면서, 이를 기하학적 측도 이론 분야에서 큰 진전이라고 칭했습니다.

네츠 카츠 교수(미국 라이스 대학교)는 "이것은 21세기 최고의 수학적 업적이 될 수 있습니다. 많은 저명한 수학자들이 해결하지 못했던 문제를 해결한 것입니다."라고 평했습니다.

두 수학자는 이전 연구를 바탕으로 스캔의 차원이 3보다 작을 가능성을 배제했습니다.