Cadangan jawapan matematik untuk peperiksaan kemasukan gred 10 di Hanoi pada tahun 2025

Jabatan Pendidikan dan Latihan Hanoi telah mengumumkan contoh soalan untuk 7 mata pelajaran untuk peperiksaan kemasukan gred ke-10 pada 2025. 7 mata pelajaran ini termasuk sastera, matematik, bahasa asing, sains semula jadi, sejarah dan geografi, sivik dan teknologi maklumat.

Peperiksaan matematik ilustrasi untuk peperiksaan kemasukan gred 10 pada tahun persekolahan 2025 di Hanoi (Tangkapan Skrin).

Untuk matematik, pengetahuan peperiksaan terdiri daripada 3 bahagian: Nombor dan algebra menyumbang 4.5 mata, geometri dan ukuran untuk 4 mata, statistik dan akaun kebarangkalian untuk 1.5 mata.

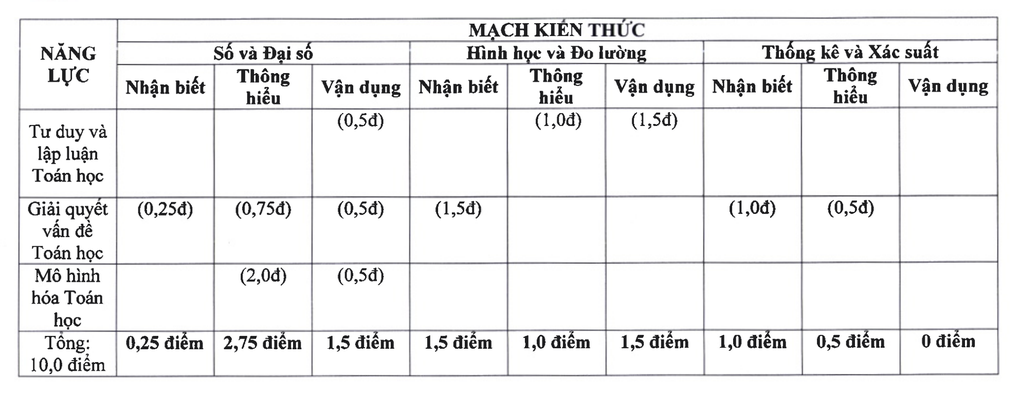
Litar pengetahuan matematik untuk peperiksaan kemasukan gred 10 di Hanoi pada 2025 (Tangkapan Skrin).

>> Lihat jawapan cadangan terperinci untuk peperiksaan matematik gred awam 10 di Hanoi pada tahun 2025 daripada guru jabatan profesional tuyensinh247 DI SINI

Semakan ujian ilustrasi matematik

Menurut guru Do Van Bao, struktur umum peperiksaan disusun seperti berikut:

Bahagian I: (1.5 mata) Termasuk 2 soalan mengenai statistik dan kebarangkalian.

- Statistik data, carta

- Kebarangkalian

Bahagian II: (1.5 mata) Termasuk 3 soalan tentang ungkapan algebra, serupa dengan Soalan I dalam peperiksaan tahun-tahun sebelumnya.

- Kira nilai ekspresi, uji kemahiran asas pelajar

- Permudahkan ungkapan

- Soalan tambahan untuk membezakan pelajar

Pelajaran III: (2.5 mata) Merangkumi 3 soalan berkaitan sistem persamaan dan persamaan kuadratik.

- Ayat 1,2: Selesaikan masalah kehidupan sebenar dengan menyediakan sistem persamaan, menyediakan persamaan

- Soalan 3 Persamaan kuadratik

Pelajaran IV. Geometri

- Geometri spatial

- Masalah tentang bulatan

Pelajaran V. Masalah lanjutan mengenai ekstrem geometri yang berkaitan dengan faktor dunia sebenar.

Jumlah markah: 10 mata, diagihkan sama rata antara bahagian pengetahuan asas dan lanjutan, daripada algebra, geometri kepada aplikasi praktikal.

Komen tentang kandungan pengetahuan

Bahagian Algebra: Termasuk kandungan asas seperti pengiraan dengan ungkapan, persamaan kuadratik dan aplikasi. Perkara baharu ujian sampel ialah terdapat banyak soalan yang mengeksploitasi masalah kehidupan sebenar, membantu pelajar mendekati masalah dalam kehidupan melalui Matematik.

Bahagian Geometri: Termasuk kandungan biasa seperti geometri satah, masalah yang berkaitan dengan bulatan dan segi empat tertera, geometri spatial, pembuktian geometri dan aplikasi geometri dalam amalan. Peperiksaan memerlukan pelajar mempunyai pemikiran spatial yang baik dan keupayaan untuk menggunakan teori geometri kepada masalah praktikal.

Bahagian Statistik dan Kebarangkalian: ialah kandungan baharu berbanding peperiksaan tahun sebelumnya, muncul dalam Pelajaran I, memerlukan pelajar menganalisis graf dan mengira kebarangkalian, iaitu kandungan dengan aplikasi praktikal dan kerap muncul dalam program buku teks baharu.

Komen tentang kesukaran

Tahap Asas dan Pertengahan: Soalan tentang menilai ungkapan, menyelesaikan persamaan kuadratik, dan mengira kebarangkalian semuanya pada tahap asas dan pertengahan. Pelajar hanya perlu mempunyai pemahaman asas yang kukuh untuk dapat melakukan soalan-soalan ini.

Tahap Lanjutan: Soalan tentang pembuktian geometri, masalah praktikal yang melibatkan geometri spatial, dan pengiraan faedah bank memerlukan pelajar mempunyai pemikiran logik yang baik dan keupayaan untuk menggunakan pengetahuan dalam amalan. Soalan-soalan ini selalunya akan mencabar bagi pelajar yang mempunyai keupayaan pembelajaran sederhana.

Contoh peperiksaan Hanoi direka bentuk untuk mengikuti program Pendidikan Am yang baharu, memfokuskan pada menguji pengetahuan dan kemahiran pelajar secara menyeluruh, terutamanya keupayaan mereka untuk menerapkannya dalam amalan.

Peperiksaan mengekalkan 60-70% daripada struktur tradisional tetapi mempunyai inovasi dalam kandungan dan kaedah membuat soalan, membantu menilai pelajar secara lebih komprehensif.

Kesukaran peperiksaan adalah sederhana, dengan perbezaan yang jelas untuk memilih pelajar yang baik.

Pada tahun-tahun sebelumnya, peperiksaan sering membezakan dengan jelas antara pelajar yang baik dan sederhana melalui soalan algebra dan geometri tulen. Peperiksaan sampel telah menambah elemen praktikal, yang memerlukan pelajar bukan sahaja mempunyai pengetahuan tetapi juga memahami cara menggunakan pengetahuan itu untuk situasi tertentu.

Struktur peperiksaan ilustrasi tahun ini telah banyak diinnovasi berbanding tahun-tahun sebelumnya, dengan klasifikasi kandungan pengetahuan dalam pelajaran, jalinan jenis soalan dan terutamanya peningkatan dalam masalah praktikal. Ini mencerminkan orientasi program pendidikan baharu, lebih memfokuskan kepada menguji keupayaan pelajar untuk mengaplikasikan pengetahuan dan mensintesis pemikiran.

Untuk berjaya dalam peperiksaan, pelajar gred 9 memerlukan:

Untuk bersedia dengan baik untuk peperiksaan kemasukan gred 10 dengan struktur dan kandungan yang sama seperti sampel peperiksaan, pelajar gred 9 perlu mengikuti langkah berikut:

1. Fahami perkara asas

Algebra: Perlu menguasai pengetahuan asas dalam program gred 9, termasuk:

Persamaan darjah satu dan kedua, penyelesaian dan sifat.

Formula berkaitan dengan satah dan geometri pepejal, terutamanya teorem yang berkaitan dengan segi tiga, bulatan, dan bentuk geometri asas.

Menyelesaikan masalah dengan menyediakan persamaan

Geometri: Pengetahuan, teorem tentang bulatan, segi empat tertera dan sifat, membuktikan segi tiga yang serupa dan menggunakan sifat segi tiga yang serupa,...

Statistik dan Kebarangkalian: Adalah perlu untuk membiasakan diri dengan konsep statistik asas seperti histogram, jadual kekerapan, pengiraan kebarangkalian mudah, kerana ini adalah bahagian yang mungkin muncul dalam peperiksaan.

2. Berlatih menyelesaikan masalah matematik sebenar

Matematik Gunaan: Pelajar perlu berlatih dengan masalah yang berkaitan dengan kehidupan sebenar, penyelesaian masalah dengan menyediakan persamaan, sistem persamaan, masalah pengeluaran dan pengurusan, atau masalah yang berkaitan dengan geometri spatial.

Mengaplikasikan pengetahuan kepada realiti: Amalkan masalah yang berkaitan dengan mengukur dan mengira isipadu dan luas dalam situasi praktikal. Ini membantu pelajar lebih memahami cara mengaplikasikan matematik dalam kehidupan.

3. Mengamalkan pemikiran logik dan kemahiran menganalisis

Pembuktian Matematik: Mengukuhkan amalan dalam masalah pembuktian geometri dan algebra. Khususnya, masalah yang memerlukan bukti hubungan antara unsur dalam satah atau geometri ruang adalah perlu untuk meningkatkan pemikiran logik.

Menganalisis dan menyelesaikan masalah: Berlatih menganalisis soalan dan memahami keperluan setiap soalan sebelum mula menyelesaikannya. Ini membantu mengelakkan kekeliruan dan meningkatkan ketepatan dalam proses pengambilan ujian.

Sumber: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm