Forskere finner løsning på klassisk geometriproblem som varte i over et århundre

Illustrasjon for geometriproblem.

Ifølge South China Morning Post har matematikeren Hong Wang – for tiden førsteamanuensis ved Courant Institute for Mathematical Sciences ved New York University (USA) – og kollegaen hans Joshua Zahl (University of British Columbia, Canada) nettopp løst et av de vanskeligste geometriproblemene i det 20.–21. århundre: Kakeya-formodningen i tredimensjonalt rom.

Hong Wang ble født i Guilin (Kina), studerte ved Peking University før han underviste og forsket i USA.

Problemet oppsto i 1917, da den japanske matematikeren Sōichi Kakeya stilte spørsmålet: «Hva er det minste arealet som kreves for å rotere en nål 180 grader? Det minimale rommet kalles 'Kakeya-settet'.»

I todimensjonalt rom er det lett å visualisere å rotere nålen for å danne en sirkel, men hvis rotasjonen er mer fleksibel, som å riste nålen mens den roterer, kan området nålen feier over være enda mindre.

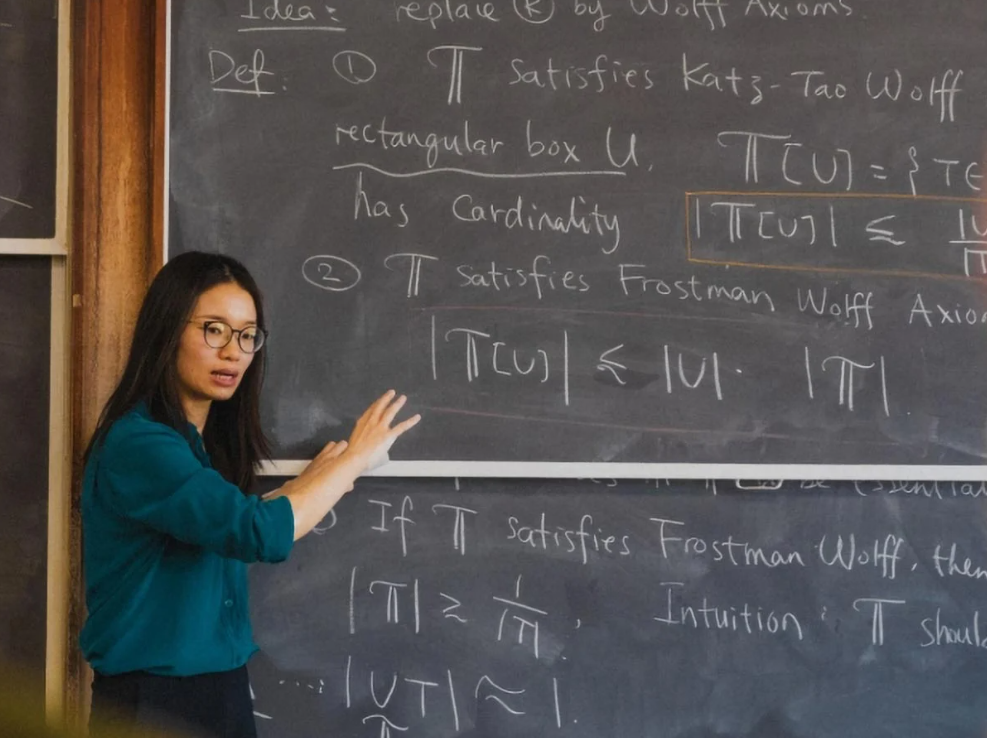
Forskere finner løsningen på et geometrisk problem som varte i mer enn et århundre.

Å flytte problemet inn i tre dimensjoner gjør det mye mer komplisert. Kakeyas formodning sier at hvis du vil rotere nålen i alle retninger, må den nødvendige plassen være stor nok i alle tre dimensjoner – du kan ikke presse den inn på et sted som er for lite eller for tynt.

I arbeidet sitt, publisert på arXiv-plattformen, beviser Wang og Zahl at området der nålen roterer i et tredimensjonalt rom ikke trenger å ha en klar form, men må fortsatt være stort nok i alle tre dimensjoner. Takket være det løste de dette problemet – dette regnes som en svært viktig oppdagelse i matematikken i dag.

Professor Terence Tao – en av verdens ledende matematikere, kalte dette «spektakulære fremskritt». Eksperter sa også at arbeidet ikke bare utvidet forståelsen av geometri, men også kunne påvirke mange felt som bildebehandling, trådløs kommunikasjon, informatikk og kryptografi – der det er ekstremt viktig å forstå bevegelser og interaksjoner i rommet.

«Det er ikke en overdrivelse, men dette er en sjelden løsning som vi har ventet på i hundrevis av år», sa matematikkprofessor Nets Katz, som underviser ved Rice University (USA).

Ifølge professor Guth Larry, foreleser ved Massachusetts Institute of Technology (USA), er Kakeya-hypotesen grunnlaget for et «tårn» av større hypoteser innen geometri. Å løse denne hypotesen vil hjelpe de høyere nivåene i kunnskapstårnet med å få muligheten til å bli nærmet og erobret.

«Jeg trodde før at dette var et enkelt, grunnleggende geometrisk problem, men i virkeligheten er dette problemet for vanskelig. Dette problemet har blitt forfulgt av mange store navn innen matematikk, men de fleste av dem oppnådde bare små resultater, var ikke systematiske og kunne ikke betraktes som en komplett løsning», delte professor Guth Larry.

Phuong Anh (Kilde: Science Daily, SCMP)

Kilde: https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-hinh-hoc-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html