Cientistas encontram solução para problema clássico de geometria que durou mais de um século

Ilustração para problema de geometria.

De acordo com o South China Morning Post, o matemático Hong Wang — atualmente professor associado do Instituto Courant de Ciências Matemáticas da Universidade de Nova York (EUA) — e seu colega Joshua Zahl (Universidade da Colúmbia Britânica, Canadá) acabaram de resolver um dos problemas de geometria mais difíceis dos séculos XX e XXI: a Conjectura de Kakeya no espaço tridimensional.

Hong Wang nasceu na cidade de Guilin (China), estudou na Universidade de Pequim antes de lecionar e pesquisar nos EUA.

O problema surgiu em 1917, quando o matemático japonês Sōichi Kakeya perguntou: "Qual é a menor área necessária para girar uma agulha 180 graus?". Esse espaço mínimo é chamado de "conjunto Kakeya".

No espaço bidimensional, girar a agulha para formar um círculo é fácil de visualizar, mas se a rotação for mais flexível, como sacudir a agulha durante a rotação, a área varrida pela agulha pode ser ainda menor.

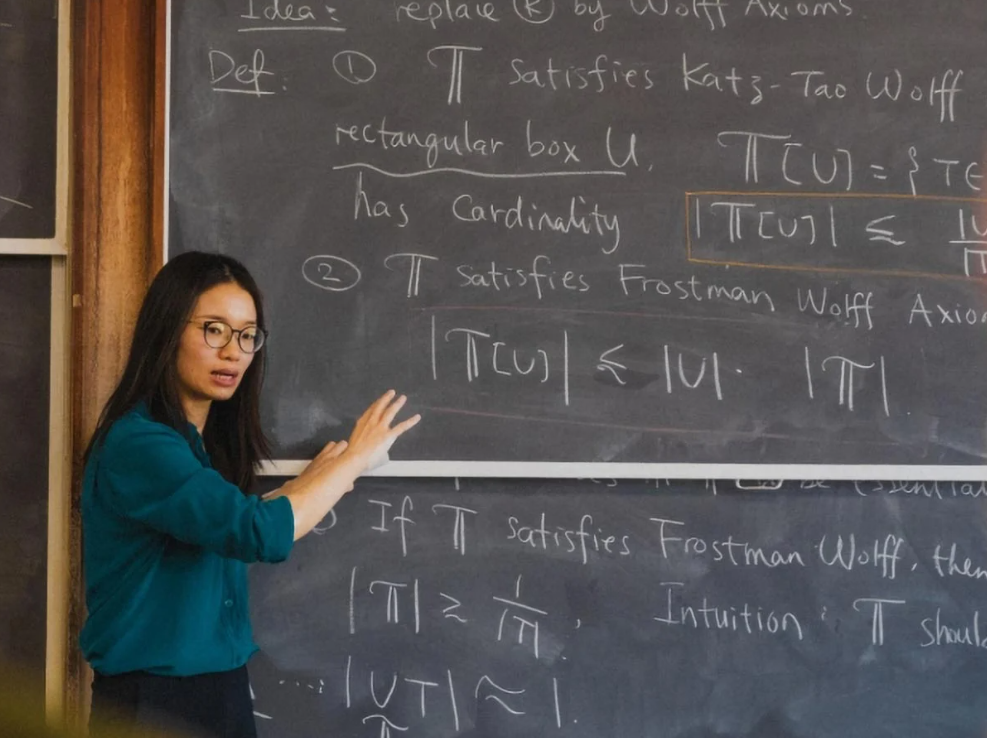
Cientistas encontram solução para problema de geometria que durou mais de um século.

Mover o problema para três dimensões o torna muito mais complicado. A conjectura de Kakeya afirma que, se você quiser girar a agulha em todas as direções, o espaço necessário deve ser grande o suficiente em todas as três dimensões – você não pode encaixá-la em um lugar muito pequeno ou muito fino.

Em seu trabalho, publicado na plataforma arXiv, Wang e Zahl provam que, no espaço tridimensional, a região na qual a agulha gira não precisa ter uma forma definida, mas ainda deve ser grande o suficiente em todas as três dimensões. Graças a isso, eles resolveram esse problema – considerado uma descoberta muito importante na matemática atual.

O professor Terence Tao, um dos principais matemáticos do mundo , chamou isso de "progresso espetacular". Especialistas também afirmaram que o trabalho não apenas expandiu a compreensão da geometria, mas também pode impactar diversas áreas, como processamento de imagens, comunicações sem fio, ciência da computação e criptografia — onde a compreensão de movimentos e interações no espaço é extremamente importante.

"Não é exagero, mas esta é uma solução rara que esperávamos há centenas de anos", disse o professor de matemática Nets Katz, que leciona na Universidade Rice (EUA).

Segundo o professor Guth Larry, do Instituto de Tecnologia de Massachusetts (EUA), a hipótese de Kakeya é a base de uma "torre" de hipóteses maiores no campo da geometria. A solução dessa hipótese ajudará os níveis mais elevados da torre do conhecimento a terem a oportunidade de serem abordados e conquistados.

"Eu costumava pensar que este era um problema geométrico simples e básico, mas, na realidade, este problema é muito difícil. Este problema foi abordado por muitos grandes nomes da matemática, mas a maioria deles alcançou apenas resultados pequenos, não eram sistemáticos e não podiam ser considerados uma solução completa", compartilhou o professor Guth Larry.

Comentário (0)