ঘুড়ি বই, গণিত ৩, খণ্ড ১-এ একটি আয়তক্ষেত্রকে ৪টি সমকোণ, ২টি সমান লম্বা বাহু এবং ২টি সমান ছোট বাহু বিশিষ্ট একটি আকৃতি হিসেবে সংজ্ঞায়িত করা হয়েছে।

একটি আয়তক্ষেত্রে একটি সমদ্বিবাহু ট্র্যাপিজয়েড এবং একটি সমান্তরালগ্রামের সমস্ত বৈশিষ্ট্য রয়েছে যেমন:
- বিপরীত বাহুর জোড়া সর্বদা সমান্তরাল এবং সমান।
- কোণ দুটি সমান এবং 90 ডিগ্রি।
- আয়তক্ষেত্রগুলির কর্ণ এবং বাহুর মধ্যবিন্দুগুলির মধ্য দিয়ে প্রতিসাম্য থাকে।
- তিনটি সমকোণ বিশিষ্ট একটি চতুর্ভুজ হল একটি আয়তক্ষেত্র।
- একটি সমকোণবিশিষ্ট সমদ্বিবাহু ট্র্যাপিজয়েড একটি আয়তক্ষেত্র।
- একটি সমকোণ বিশিষ্ট একটি সমান্তরালগ্রাম হল একটি আয়তক্ষেত্র।
- দুটি সমান কর্ণবিশিষ্ট একটি মুখমন্ডল একটি আয়তক্ষেত্র।
গণিত ৩য় পাঠ্যপুস্তক অনুসারে, একটি আয়তক্ষেত্রের পরিধি গণনা করার জন্য, আমরা দৈর্ঘ্য এবং প্রস্থ (পরিমাপের একই একক) নিই এবং তারপর ২ দিয়ে গুণ করি।
| P = (a+b) x 2 |
সেখানে
P হল আয়তক্ষেত্রের পরিধি।
a হল আয়তক্ষেত্রের দৈর্ঘ্য।
b হলো আয়তক্ষেত্রের প্রস্থ।

উদাহরণস্বরূপ: 6 সেমি দৈর্ঘ্য এবং 4 সেমি প্রস্থ বিশিষ্ট একটি আয়তক্ষেত্রের পরিধি গণনা করো।
উত্তর: আয়তক্ষেত্রের পরিধি হল P = (6+4) x 2 = 20 (সেমি)।
আয়তক্ষেত্র এবং বর্গক্ষেত্রের তুলনা করুন
| মানদণ্ড | আয়তক্ষেত্র | বর্গক্ষেত্র |
|---|---|---|
| প্রান্ত | ৪টি বাহু, ২ জোড়া বিপরীত বাহু সমান | ৪টি দিক, ৪টি দিকই সমান |
| কোণ | ৪টি সমকোণ | ৪টি সমকোণ |
| তির্যক | দুটি কর্ণ সমান, মধ্যবিন্দুতে ছেদ করে কিন্তু লম্ব নয় | দুটি কর্ণ সমান, মধ্যবিন্দুতে ছেদ করে এবং একে অপরের সাথে লম্ব। |
| পরিধি গণনার সূত্র | P = (a+b) x 2 | পি = 4a |
| ক্ষেত্রফল গণনার সূত্র | S = অক্ষ | S = a2 |
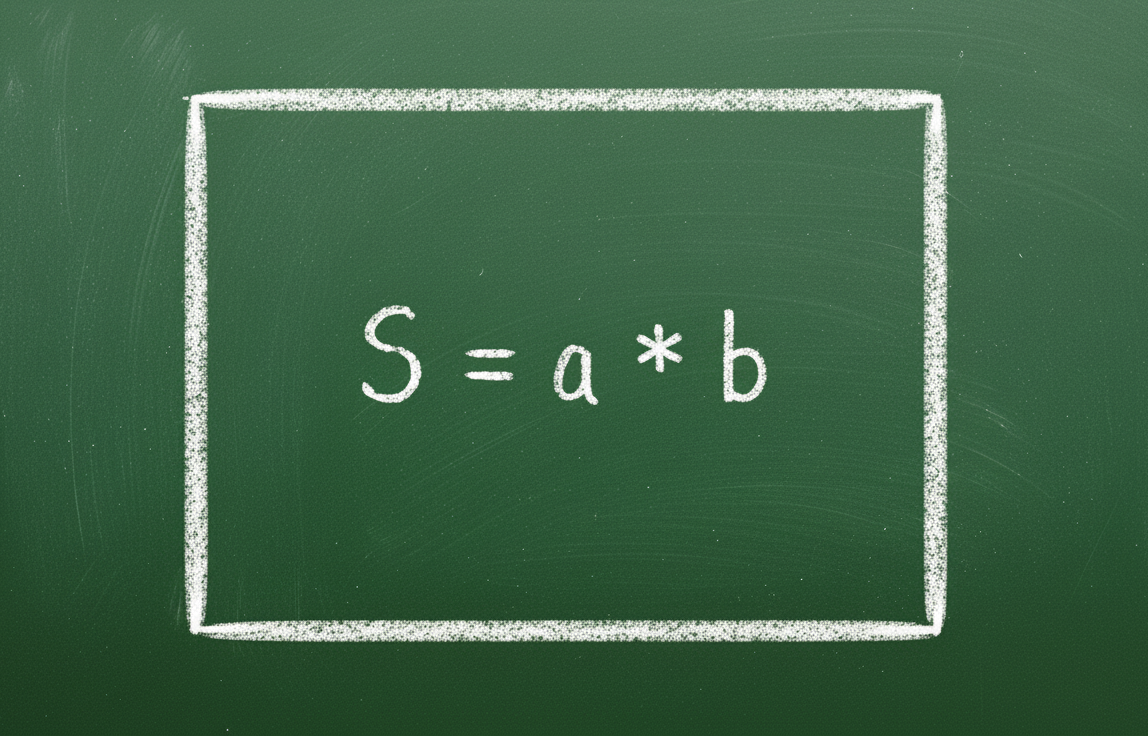
সূত্র: https://vietnamnet.vn/cong-thuc-tinh-chu-vi-hinh-chu-nhat-la-gi-2452851.html


![[ছবি] পার্টির কেন্দ্রীয় কার্যালয়ের ঐতিহ্যবাহী দিবসের ৯৫তম বার্ষিকীতে যোগদান করছেন সাধারণ সম্পাদক টু ল্যাম](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760784671836_a1-bnd-4476-1940-jpg.webp)
![[ছবি] হ্যানয় পার্টি কমিটির ১৮তম কংগ্রেসের সমাপনী অনুষ্ঠান](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/17/1760704850107_ndo_br_1-jpg.webp)



![[ছবি] বর্জ্য সংগ্রহ, সবুজ বীজ বপন](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760786475497_ndo_br_1-jpg.webp)


























































































মন্তব্য (0)