Forskare hittar lösning på klassiskt geometriproblem som varade i mer än ett sekel

Illustration för geometriproblem.

Enligt South China Morning Post har matematikern Hong Wang – för närvarande docent vid Courant Institute for Mathematical Sciences vid New York University (USA) – och hans kollega Joshua Zahl (University of British Columbia, Kanada) just löst ett av de svåraste geometriproblemen under 1900- och 2000-talen: Kakeya-förmodandet i tredimensionellt rum.

Hong Wang föddes i Guilin (Kina), studerade vid Pekings universitet innan han undervisade och forskade i USA.

Problemet uppstod 1917, när den japanske matematikern Sōichi Kakeya ställde frågan: "Vilken är den minsta area som krävs för att rotera en nål 180 grader? Det minimala utrymmet kallas 'Kakeya-mängden'."

I tvådimensionellt rum är det lätt att visualisera att rotera nålen för att bilda en cirkel, men om rotationen är mer flexibel, som att skaka nålen medan den roterar, kan det område som nålen sveper över vara ännu mindre.

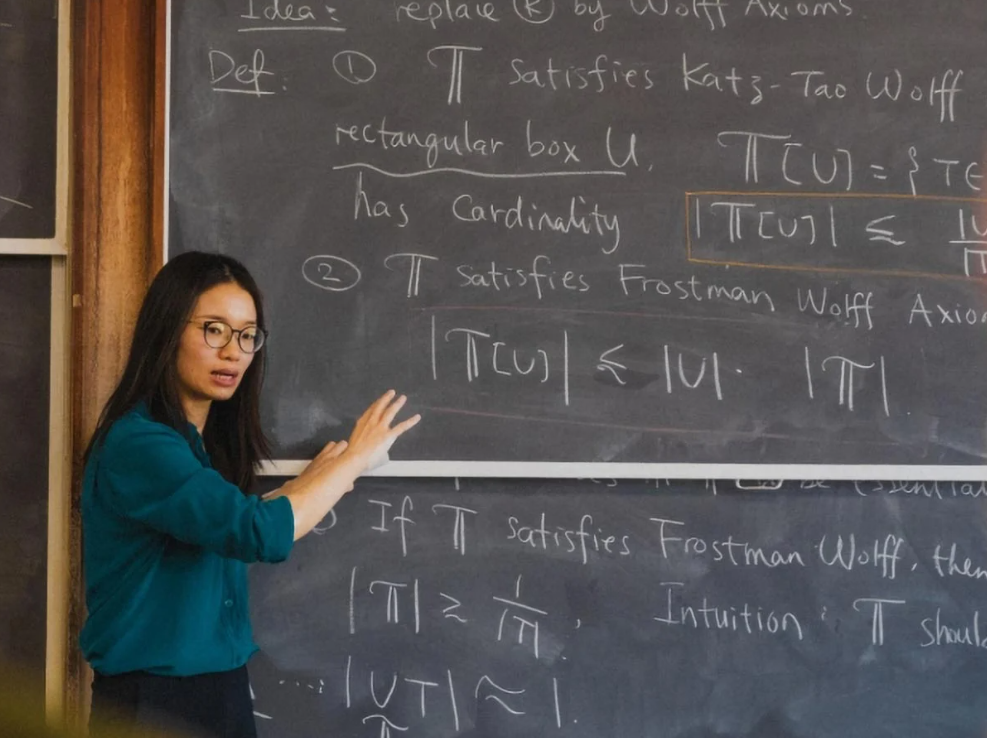
Forskare hittar lösning på ett geometriskt problem som varade i mer än ett sekel.

Att flytta problemet till tre dimensioner gör det mycket mer komplicerat. Kakeyas hypotes säger att om man vill rotera nålen i alla riktningar måste det utrymme som behövs vara tillräckligt stort i alla tre dimensioner – man kan inte klämma in det på en plats som är för liten eller för tunn.

I sitt arbete, publicerat på arXiv-plattformen, bevisar Wang och Zahl att området där nålen roterar i ett tredimensionellt rum inte behöver ha en tydlig form, utan måste ändå vara tillräckligt stort i alla tre dimensioner. Tack vare det löste de problemet – detta anses vara en mycket viktig upptäckt inom matematiken idag.

Professor Terence Tao – en av världens ledande matematiker, kallade detta "spektakulära framsteg". Experter sa också att arbetet inte bara utökade förståelsen av geometri utan också skulle kunna påverka många områden som bildbehandling, trådlös kommunikation, datavetenskap och kryptografi – där det är oerhört viktigt att förstå rörelser och interaktioner i rymden.

”Det är ingen överdrift, men det här är en sällsynt lösning som vi har väntat på i hundratals år”, säger matematikprofessorn Nets Katz, som undervisar vid Rice University (USA).

Enligt professor Guth Larry, föreläsare vid Massachusetts Institute of Technology (USA), är Kakeya-hypotesen grunden för ett "torn" av större hypoteser inom geometrin. Att lösa denna hypotes kommer att hjälpa de högre nivåerna i kunskapstornet att få möjlighet att närmas och erövras.

"Jag trodde tidigare att det här var ett enkelt, grundläggande geometriproblem, men i verkligheten är problemet för svårt. Många stora namn inom matematiken har arbetat med det här problemet, men de flesta av dem uppnådde bara små resultat, var inte systematiska och kunde inte betraktas som en komplett lösning", delade professor Guth Larry.

Phuong Anh (Källa: Science Daily, SCMP)

Källa: https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-hinh-hoc-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html