Javasolt válaszok a 2025-ös hanoi 10. osztályos felvételi vizsga minta matematika tesztjéhez.

A Hanoi Oktatási és Képzési Minisztérium közzétette a 2025-ös állami iskolák 10. osztályos felvételi vizsgájának 7 tantárgyból álló mintavizsga-kérdéseit. Ez a 7 tantárgy a következő: vietnami irodalom, matematika, idegen nyelv, természettudományok, történelem és földrajz, állampolgári ismeretek, valamint informatika.

Mintavizsgadolgozat a 2025-ös tanév 10. osztályos felvételi vizsgájához Hanoiban (képernyőkép).

Matematika esetében a vizsga tartalma három részre oszlik: számok és algebra (4,5 pont), geometria és mérés (4 pont), valamint statisztika és valószínűségszámítás (1,5 pont).

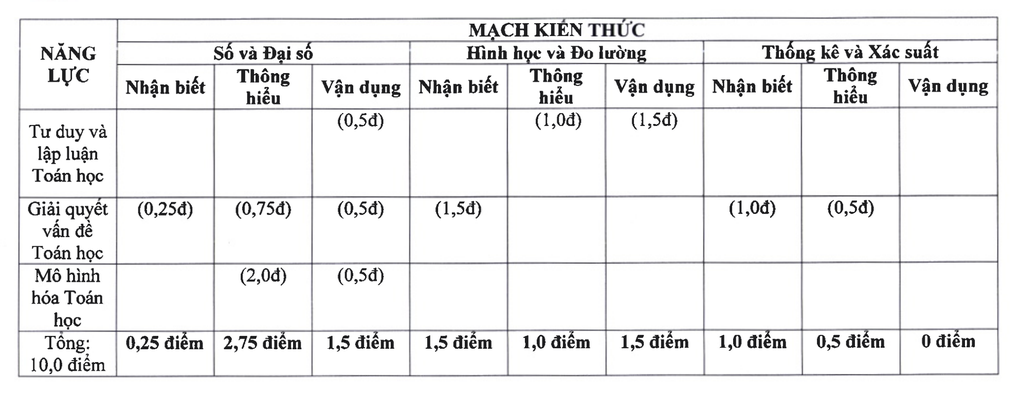
A 2025-ös hanoi 10. osztályos felvételi vizsga tanterve (képernyőkép).

>> Tekintse meg a tuyensinh247 szakértői csapatának részletes válaszjavaslatait a 2025-ös hanoi állami középiskolai matematika felvételi vizsgára ITT

A minta matematika vizsga áttekintése

Do Van Bao tanár értékelése szerint a vizsga általános szerkezete a következőképpen alakul:

I. rész: (1,5 pont) 2 statisztikai és valószínűségszámítási kérdésből áll.

- Adatstatisztikák, diagramok

- Valószínűség

II. rész: (1,5 pont) 3 kérdésből áll az algebrai kifejezésekkel kapcsolatban, hasonlóan az előző évek vizsgáinak I. részéhez.

- Kifejezések értékelése, a tanulók alapvető készségeinek tesztelése.

- Egyszerűsítsd a kifejezést

- Kiegészítő kérdések a tanulók megkülönböztetése érdekében

III. rész: (2,5 pont) 3 kérdésből áll, amelyek egyenletrendszerekkel és másodfokú egyenletekkel kapcsolatosak.

- 1. és 2. kérdés: Valós problémák megoldása egyenletrendszerek és egyenletek felállításával.

- 3. kérdés: Másodfokú egyenletek

IV. lecke. Geometria

- Térbeli geometria

- Körökkel kapcsolatos problémák

V. lecke. Haladó szintű feladatok geometriai szélsőértékekkel, valós alkalmazásokkal.

Összpontszám: 10 pont, egyenletesen elosztva az alap- és haladó tudásterületek között, az algebrától és a geometriától a gyakorlati alkalmazásokig.

Megjegyzések a tudástárhoz

Algebra rész: Alapvető tartalmakat tartalmaz, mint például kifejezésekkel végzett számítások, másodfokú egyenletek és alkalmazások. A minta teszt újdonsága, hogy számos olyan kérdést tartalmaz, amelyek valós problémákat vizsgálnak, segítve a diákokat az élettel kapcsolatos kérdések matematikai megközelítésében.

Geometria rész: Ismert témákat tartalmaz, mint például a síkgeometria, a körökkel és beírt négyszögekkel kapcsolatos problémák, a térbeli geometria, a geometriai bizonyítások és a geometria alkalmazása a való életben. A vizsga megköveteli a hallgatóktól, hogy meglehetősen jó térbeli gondolkodással rendelkezzenek, és képesek legyenek a geometriai elméletet gyakorlati problémákra alkalmazni.

A Statisztika és valószínűségszámítás rész új tartalommal bővült a korábbi évek vizsgáihoz képest, és az 1. leckében jelent meg. A tanulóknak grafikonokat kell elemezniük és valószínűségeket kell kiszámítaniuk, amelyek gyakorlati alkalmazások, és gyakran szerepelnek az új tankönyvi tananyagban.

Megjegyzések a nehézségi szintről

Alap- és középhaladó szint: A kifejezések kiértékelésével, a másodfokú egyenletek megoldásával és a valószínűségszámítással kapcsolatos kérdések mind alap- és középhaladó szintűek. A tanulóknak csak az alapvető ismereteket kell elsajátítaniuk ahhoz, hogy meg tudják válaszolni ezeket a kérdéseket.

Haladó szint: A geometriai bizonyításokat, a térbeli geometriával kapcsolatos gyakorlati problémákat és a banki kamatláb-számításokat tartalmazó kérdések erős logikus gondolkodási készségeket és a tudás valós helyzetekben való alkalmazásának képességét igénylik a diákoktól. Ezek a kérdések gyakran kihívást jelentenek az átlagos tanulmányi képességű diákok számára.

Hanoi mintavizsgája szorosan követi az új általános oktatási tantervet, a diákok tudásának és készségeinek átfogó tesztelésére összpontosítva, különös tekintettel arra, hogy mennyire képesek ezeket valós helyzetekben alkalmazni.

A vizsga megtartotta hagyományos szerkezetének 60-70%-át, de a tartalom és a kérdések formátuma tekintetében újításokat eszközöltek, amelyek segítenek a diákok átfogóbb értékelésében.

A vizsga nehézségi szintje közepes, egyértelmű differenciálással a kiemelkedő teljesítményű diákok kiválasztása érdekében.

A korábbi években a vizsga gyakran egyértelműen megkülönböztette a kiemelkedő és az átlagos tanulókat pusztán algebrai és geometriai kérdések révén. A mintavizsga gyakorlati elemmel is bővült, és nemcsak a tudás megszerzését követeli meg a tanulóktól, hanem azt is, hogy megértsék, hogyan alkalmazzák ezt a tudást konkrét helyzetekben.

Az idei mintavizsga szerkezete jelentős változásokon ment keresztül az előző évekhez képest, az egyes kérdéseken belüli tudástartalom osztályozásával, a kérdéstípusok váltakozó mintázatával, és különösen a gyakorlati feladatok számának növekedésével. Ez pontosan tükrözi az új oktatási program irányát, amely jobban a diákok tudásalkalmazási és információszintézis-képességének tesztelésére összpontosít.

A vizsgán való jó szerepléshez a kilencedikes tanulóknak a következőkre van szükségük:

A 10. osztályos felvételi vizsgára való jó felkészüléshez, amelynek szerkezete és tartalma hasonló a mintavizsgához, a 9. osztályos tanulóknak a következő lépéseket kell követniük:

1. Sajátítsa el az alapvető ismereteket.

Algebra: El kell sajátítanod a 9. osztályos tanterv alapfogalmait, beleértve:

Lineáris és másodfokú egyenletek: megoldási módszerek és tulajdonságaik.

A képletek a sík- és térbeli geometriára vonatkoznak, különösen a háromszögekre, körökre és alapvető geometriai alakzatokra vonatkozó tételekre.

Oldd meg a problémát egy egyenlet felállításával.

Geometria: Ismeretek és tételek körökről, beírt négyszögekről és tulajdonságokról, hasonló háromszögek bizonyítása és hasonló háromszögek tulajdonságainak alkalmazásai,...

Statisztika és valószínűségszámítás: Meg kell ismerkedni az alapvető statisztikai fogalmakkal, mint például a gyakorisági diagramok, gyakorisági táblázatok és egyszerű valószínűségszámítások, mivel ez egy olyan rész, amely megjelenhet a vizsgán.

2. Gyakorold a valós problémák megoldását.

Alkalmazott matematika: A hallgatóknak valós élethelyzetekhez kapcsolódó problémákkal, problémamegoldó módszerekkel, például egyenletek és egyenletrendszerek felállításával, termeléssel és irányítással kapcsolatos problémákkal, vagy térbeli geometriával kapcsolatos problémákkal kell gyakorolniuk.

A tudás alkalmazása valós helyzetekben: Gyakorolja a térfogat és terület mérésével és kiszámításával kapcsolatos problémák megoldását gyakorlati helyzetekben. Ez segít a tanulóknak jobban megérteni, hogyan alkalmazzák a matematikát a gyakorlatban.

3. Logikus gondolkodás és elemző készségek fejlesztése.

Matematikai bizonyítások: A geometriai és algebrai bizonyítási feladatok gyakorlásának erősítése. Különösen azok a feladatok elengedhetetlenek a logikus gondolkodás fejlesztéséhez, amelyek síkbeli vagy térbeli geometriában lévő elemek közötti kapcsolatok bizonyítását igénylik.

Elemzés és problémamegoldás: Gyakorold a probléma elemzését, és értsd meg az egyes kérdések követelményeit, mielőtt megpróbálod megoldani. Ez segít elkerülni a zavart és növeli a pontosságot a vizsga során.

Forrás: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm