Naukowcy znaleźli rozwiązanie klasycznego problemu geometrycznego, który trwał ponad wiek

Ilustracja do zadania geometrycznego.

Jak donosi gazeta South China Morning Post, matematyk Hong Wang – obecnie profesor nadzwyczajny w Instytucie Nauk Matematycznych Couranta na Uniwersytecie Nowojorskim (USA) – i jego kolega Joshua Zahl (Uniwersytet Kolumbii Brytyjskiej, Kanada) właśnie rozwiązali jeden z najtrudniejszych problemów geometrycznych XX–XXI wieku: hipotezę Kakeya w przestrzeni trójwymiarowej.

Hong Wang urodził się w mieście Guilin (Chiny), studiował na Uniwersytecie Pekińskim, a następnie wykładał i prowadził badania w USA.

Problem narodził się w 1917 roku, kiedy japoński matematyk Sōichi Kakeya zadał pytanie: „Jaka jest najmniejsza powierzchnia potrzebna do obrócenia igły o 180 stopni?”. Ta minimalna powierzchnia nazywana jest „zbiorem Kakeya”.

W przestrzeni dwuwymiarowej obrót igły tak, aby utworzyła okrąg, jest łatwy do zwizualizowania, ale jeśli obrót jest bardziej elastyczny, np. poprzez potrząsanie igłą podczas obrotu, obszar, jaki igła przemierza, może być jeszcze mniejszy.

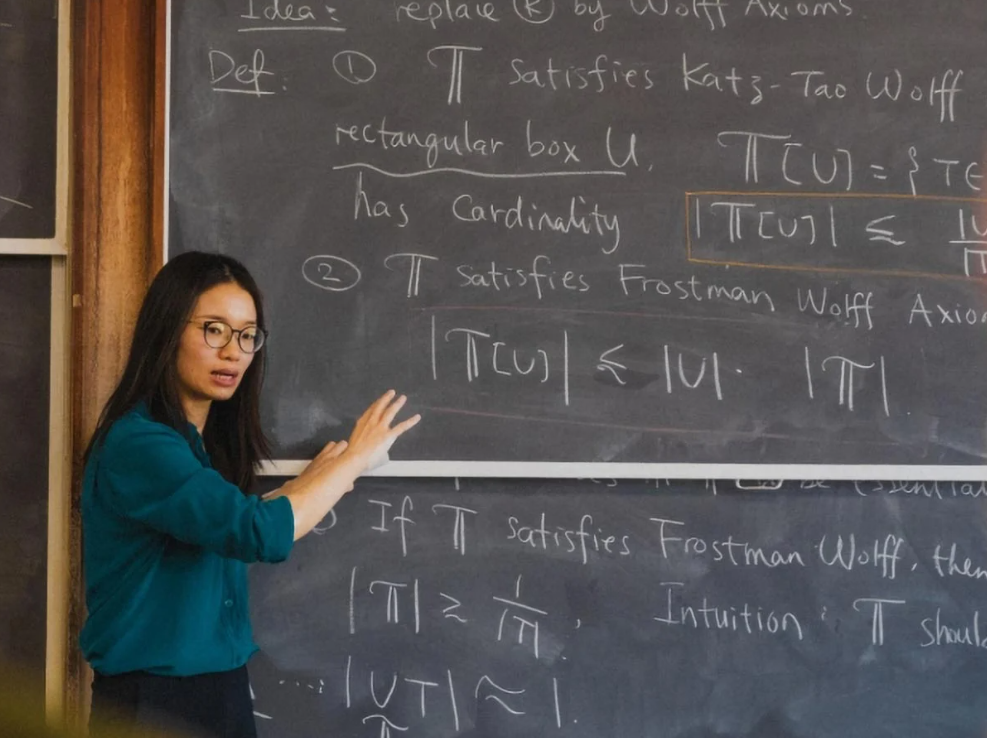
Naukowcy znaleźli rozwiązanie problemu geometrycznego, który trwał ponad wiek.

Przeniesienie problemu do trzech wymiarów znacznie go komplikuje. Hipoteza Kakeyi głosi, że aby obrócić igłę we wszystkich kierunkach, potrzebna przestrzeń musi być wystarczająco duża we wszystkich trzech wymiarach – nie da się jej wcisnąć w miejsce, które jest zbyt małe lub zbyt wąskie.

W swojej pracy, opublikowanej na platformie arXiv, Wang i Zahl dowodzą, że w przestrzeni trójwymiarowej obszar, w którym obraca się igła, nie musi mieć określonego kształtu, lecz musi być wystarczająco duży we wszystkich trzech wymiarach. Dzięki temu rozwiązali ten problem – jest to dziś uważane za niezwykle ważne odkrycie w matematyce.

Profesor Terence Tao – jeden z czołowych matematyków na świecie – nazwał to „spektakularnym postępem”. Eksperci stwierdzili również, że praca ta nie tylko poszerzyła wiedzę z zakresu geometrii, ale może również wpłynąć na wiele dziedzin, takich jak przetwarzanie obrazu, komunikacja bezprzewodowa, informatyka i kryptografia – gdzie zrozumienie ruchów i interakcji w przestrzeni jest niezwykle ważne.

„To nie przesada, ale jest to rzadkie rozwiązanie, na które czekaliśmy setki lat” – powiedział profesor matematyki Nets Katz, który wykłada na Uniwersytecie Rice’a (USA).

Według profesora Gutha Larry'ego, wykładowcy z Massachusetts Institute of Technology (USA), hipoteza Kakeya stanowi fundament „wieży” większych hipotez w dziedzinie geometrii. Rozwiązanie tej hipotezy pomoże w zbliżeniu się do wyższych poziomów wieży wiedzy i ich zdobyciu.

„Kiedyś myślałem, że to prosty, podstawowy problem geometryczny, ale w rzeczywistości jest on zbyt trudny. Z tym problemem zmagało się wielu wybitnych matematyków, ale większość z nich osiągnęła jedynie mierne rezultaty, nie była systematyczna i nie można jej uznać za kompletne rozwiązanie” – powiedział profesor Guth Larry.

Phuong Anh (Źródło: Science Daily, SCMP)

Source: https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-hinh-hoc-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html