Förslag på mattesvar för inträdesprovet för årskurs 10 i Hanoi år 2025

Hanois utbildningsdepartement har tillkännagivit exempelfrågor för 7 ämnen inför inträdesprovet för årskurs 10 år 2025. Dessa 7 ämnen inkluderar litteratur, matematik, främmande språk, naturvetenskap, historia och geografi, samhällskunskap och informationsteknik.

Illustrativt matteprov för inträdesprovet för årskurs 10 läsåret 2025 i Hanoi (skärmdump).

För matematik består kunskaperna i provet av tre delar: Tal och algebra står för 4,5 poäng, geometri och mätning står för 4 poäng, statistik och sannolikhet står för 1,5 poäng.

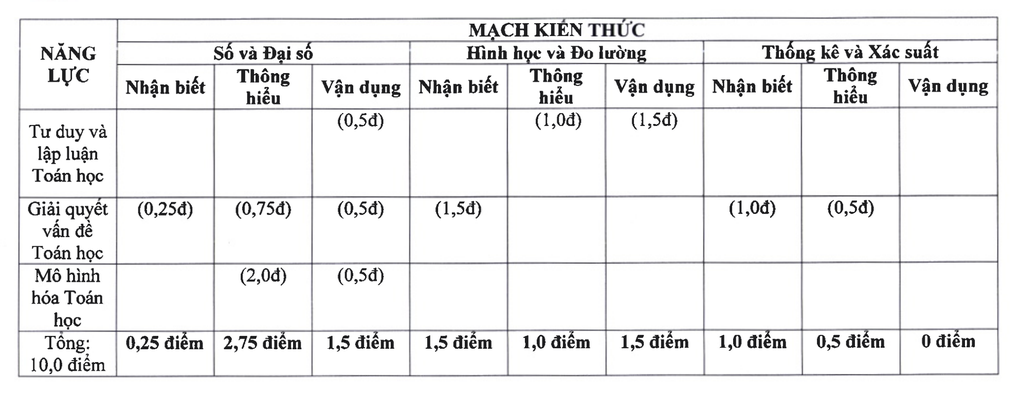
Matematikkunskapskrets för inträdesprovet för årskurs 10 i Hanoi år 2025 (skärmdump).

>> Se detaljerade förslag på svar för matteprovet för årskurs 10 i Hanoi år 2025 från lärare vid yrkesavdelningen tuyensinh247 HÄR

Granskning av illustrationstest i matematik

Enligt läraren Do Van Bao är provets allmänna struktur upplagd enligt följande:

Del I: (1,5 poäng) Innehåller 2 frågor om statistik och sannolikhet.

- Datastatistik, diagram

- Sannolikhet

Del II: (1,5 poäng) Innehåller 3 frågor om algebraiska uttryck, liknande fråga I i tidigare års prov.

- Beräkna uttrycksvärden, testa elevernas grundläggande färdigheter

- Förenkla uttrycket

- Ytterligare frågor för att differentiera eleverna

Lektion III: (2,5 poäng) Innehåller 3 frågor relaterade till ekvationssystem och andragradsekvationer.

- Mening 1,2: Lös verkliga problem genom att ställa upp ett ekvationssystem, ställa upp ekvationer

- Fråga 3 Andragradsekvation

Lektion IV. Geometri

- Rumslig geometri

- Problem med cirklar

Lektion V. Avancerade problem med geometriska extremer relaterade till verkliga faktorer.

Totalpoäng: 10 poäng, jämnt fördelat mellan grundläggande och avancerade kunskapsavsnitt, från algebra, geometri till praktiska tillämpningar.

Kommentarer om kunskapsinnehåll

Algebraavsnitt: Innehåller grundläggande innehåll såsom beräkningar med uttryck, andragradsekvationer och tillämpningar. Det nya med exempelprovet är att det finns många frågor som utnyttjar verkliga problem och hjälper eleverna att närma sig problem i livet genom matematik.

Geometriavsnitt: Innehåller välbekant innehåll såsom plangeometri, problem relaterade till cirklar och inskrivna fyrhörningar, rumslig geometri, geometriska bevis och geometriska tillämpningar i praktiken. Examinationen kräver att studenterna har gott rumsligt tänkande och förmåga att tillämpa geometrisk teori på praktiska problem.

Statistik- och sannolikhetsavsnitt: är nytt innehåll jämfört med föregående års prov, som finns i lektion I och kräver att eleverna analyserar grafer och beräknar sannolikhet, vilket är tillfredsställande med praktisk tillämpning och ofta förekommer i nya läroboksprogram.

Kommentarer om svårighetsgrad

Grundläggande och mellanliggande nivå: Frågor om att utvärdera uttryck, lösa andragradsekvationer och beräkna sannolikhet finns alla på grundläggande och mellanliggande nivå. Eleverna behöver bara ha en god förståelse för grunderna för att kunna göra dessa frågor.

Avancerad nivå: Frågor om geometriska bevis, praktiska problem som involverar rumslig geometri och bankränteberäkningar kräver att eleverna har gott logiskt tänkande och förmåga att tillämpa kunskap i praktiken. Dessa frågor kommer ofta att vara utmanande för elever med genomsnittlig inlärningsförmåga.

Hanois exempelprov är utformat för att noggrant följa det nya allmänna utbildningsprogrammet, med fokus på att heltäckande testa elevernas kunskaper och färdigheter, särskilt deras förmåga att tillämpa dem i praktiken.

Examinationen behåller 60–70 % av den traditionella strukturen men har innovationer i innehåll och frågeformuleringsmetoder, vilket hjälper till att utvärdera studenterna mer heltäckande.

Examenssvårighetsgraden är medelhög, med tydlig differentiering för att välja ut duktiga studenter.

Tidigare år gjorde provet ofta tydlig skillnad mellan duktiga och medelmåttiga elever genom rena algebra- och geometrifrågor. Exempelprovet har lagt till praktiska inslag, vilket kräver att eleverna inte bara har kunskap utan också förstår hur man tillämpar den kunskapen i specifika situationer.

Strukturen för årets illustrativa prov har i hög grad förnyats jämfört med tidigare år, med en klassificering av kunskapsinnehåll i lektionerna, en sammanflätning av olika typer av frågor och särskilt en ökning av praktiska problem. Detta återspeglar inriktningen på det nya utbildningsprogrammet, som fokuserar mer på att testa elevernas förmåga att tillämpa kunskap och syntetisera tänkande.

För att klara provet bra behöver elever i årskurs 9:

För att förbereda sig väl för inträdesprovet för årskurs 10, med samma struktur och innehåll som exempelprovet, behöver elever i årskurs 9 följa dessa steg:

1. Förstå grunderna

Algebra: Behöver behärska grundläggande kunskaper i 9:e klassprogrammet, inklusive:

Första och andra gradens ekvationer, lösningar och egenskaper.

Formler relaterade till plan och solid geometri, särskilt satser relaterade till trianglar, cirklar och grundläggande geometriska former.

Lös problem genom att ställa upp ekvationer

Geometri: Kunskap, satser om cirklar, inskrivna fyrhörningar och egenskaper, bevis av likformiga trianglar och tillämpning av egenskaper hos likformiga trianglar,...

Statistik och sannolikhet: Det är nödvändigt att vara bekant med grundläggande statistiska begrepp som histogram, frekvenstabeller och enkla sannolikhetsberäkningar, eftersom dessa är avsnitt som kan förekomma i provet.

2. Öva på att lösa riktiga matteproblem

Tillämpad matematik: Eleverna behöver öva på problem relaterade till verkligheten, problemlösning genom att ställa upp ekvationer, ekvationssystem, produktions- och hanteringsproblem eller problem relaterade till rumslig geometri.

Att tillämpa kunskap i verkligheten: Öva på problem relaterade till att mäta och beräkna volym och area i praktiska situationer. Detta hjälper eleverna att bättre förstå hur man tillämpar matematik i livet.

3. Öva logiskt tänkande och analytiska färdigheter

Matematiskt bevis: Stärk övningen i geometriska och algebraiska bevisproblem. I synnerhet är problem som kräver bevis på samband mellan element i ett plan eller rumslig geometri nödvändiga för att förbättra logiskt tänkande.

Analysera och lös problem: Öva på att analysera frågorna och förstå kraven för varje fråga innan du börjar lösa dem. Detta hjälper till att undvika förvirring och ökar noggrannheten i testprocessen.

Källa: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm