ایک مستطیل کے دائرے کا حساب لگانے کا فارمولا کیا ہے؟

مستطیل کی تعریف

کائٹ بک، ریاضی 3، والیم 1 مستطیل کو ایک شکل کے طور پر بیان کرتا ہے جس میں 4 دائیں زاویے، 2 مساوی لمبے اطراف اور 2 برابر چھوٹے اطراف ہوتے ہیں۔

مستطیل کی خصوصیات

ایک مستطیل میں ایک isosceles trapezoid اور ایک متوازی علامت کی تمام خصوصیات ہیں جیسے:

- مخالف سمتوں کے جوڑے ہمیشہ متوازی اور برابر ہوتے ہیں۔

- زاویے برابر اور 90 ڈگری ہیں۔

- مستطیلوں میں اخترن اور اطراف کے وسط پوائنٹس کے ذریعے ہم آہنگی ہوتی ہے۔

مستطیل کو پہچاننے کے لیے نشانیاں

- تین دائیں زاویوں والا چوکور مستطیل ہے۔

- ایک دائیں زاویہ کے ساتھ ایک آئوسیلس ٹریپیزائڈ ایک مستطیل ہے۔

- ایک دائیں زاویہ کے ساتھ متوازی علامت ایک مستطیل ہے۔

- دو مساوی اخترن والا چہرہ مستطیل ہے۔

ایک مستطیل کے فریم کا حساب لگانے کا فارمولا

ریاضی 3 کی نصابی کتاب کے مطابق، مستطیل کے دائرے کا حساب لگانے کے لیے، ہم لمبائی کے علاوہ چوڑائی (پیمائش کی ایک ہی اکائی) لیتے ہیں اور پھر 2 سے ضرب کرتے ہیں۔

P = (a+b) x 2

وہاں

P مستطیل کا دائرہ ہے۔

a مستطیل کی لمبائی ہے۔

b مستطیل کی چوڑائی ہے۔

مثال کے طور پر: 6 سینٹی میٹر لمبائی اور چوڑائی 4 سینٹی میٹر کے ساتھ مستطیل کے دائرے کا حساب لگائیں۔

جواب: مستطیل کا دائرہ P = (6+4) x 2 = 20 (سینٹی میٹر) ہے۔

مستطیل اور مربع کا موازنہ کریں۔

معیار	مستطیل	مربع
کنارہ	4 اطراف، مخالف اطراف کے 2 جوڑے برابر ہیں۔	4 اطراف، تمام 4 اطراف برابر ہیں۔
گوشہ	4 صحیح زاویہ	4 صحیح زاویہ
ترچھا ۔	دو اخترن برابر ہیں، درمیانی نقطہ پر آپس میں ہیں لیکن کھڑے نہیں ہیں۔	دو اخترن برابر ہیں، درمیانی نقطہ پر ایک دوسرے کو کاٹتے ہیں اور ایک دوسرے کے لیے کھڑے ہیں۔
دائرہ شمار کرنے کا فارمولا	P = (a+b) x 2	P = 4a
رقبہ کا حساب لگانے کا فارمولا	S = axb	S = a2

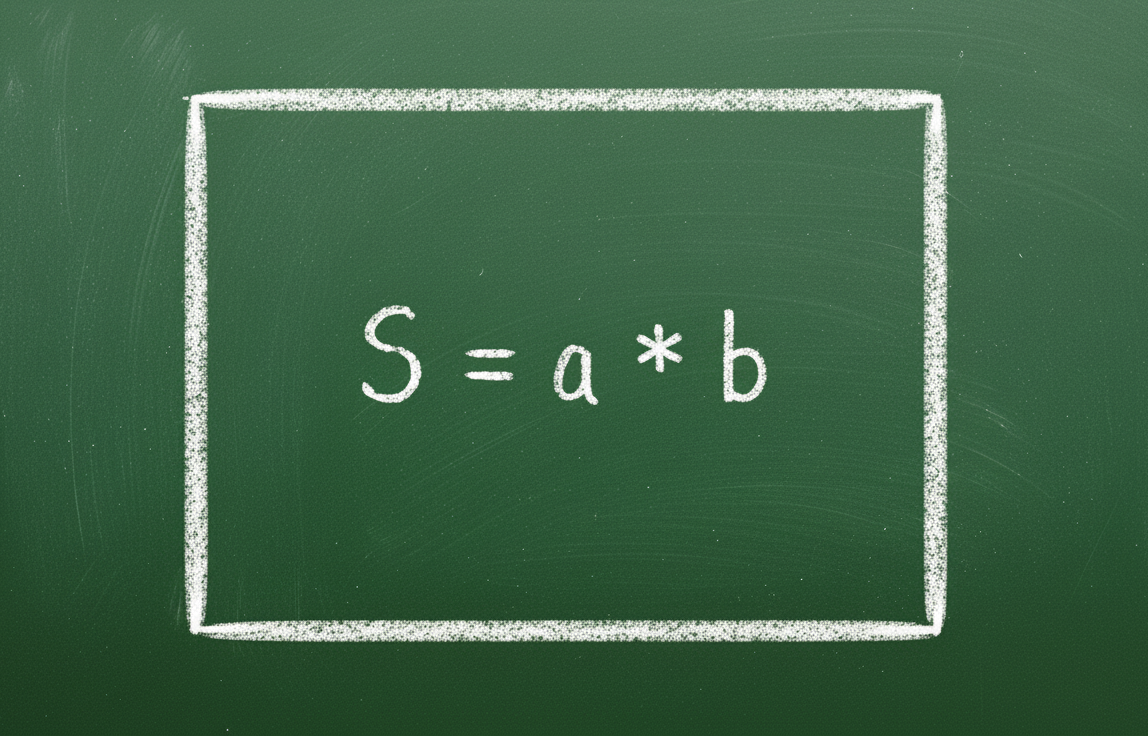
مستطیل کے رقبے کا حساب لگانے کا فارمولہ مستطیل کے رقبہ کا حساب لگانے کے لیے لمبائی کو چوڑائی سے ضرب دینے کے علاوہ ایک طرف کو جان کر اور اخترن یا دائرہ کو شامل کرتے ہوئے بھی اس کا حساب لگایا جا سکتا ہے۔

ماخذ: https://vietnamnet.vn/cong-thuc-tinh-chu-vi-hinh-chu-nhat-la-gi-2452851.html