مستطیل کے رقبہ کا حساب لگانے کا فارمولا

مستطیل کے رقبے کا حساب لگانے کے لیے، لمبائی کو چوڑائی سے ضرب دینے کے علاوہ، آپ اس کا ایک رخ جان کر اور اخترن یا دائرہ کا اضافہ کر کے بھی حساب لگا سکتے ہیں۔

فوری جائزہ:

• مستطیل کیا ہے؟
• مستطیل کے رقبہ کا حساب لگانے کا فارمولا
• مستطیل کے رقبہ کا حساب لگانے کا فارمولا جب ایک طرف اور اخترن معلوم ہوں۔
• دائرہ معلوم کرتے وقت مستطیل کے رقبے کا حساب لگانے کا فارمولا
• مستطیل کو پہچاننے کے لیے نشانیاں؟
• کیا مستطیل ایک متوازی علامت ہے؟
• کیا ایک مستطیل ایک isosceles trapezoid ہے؟

مستطیل کیا ہے؟

ویتنام ایجوکیشن پبلشنگ ہاؤس کی نصابی کتاب سیریز "علم کو زندگی سے جوڑنا" کے سبق 13، ریاضی 8 (جلد 1) کے مطابق، مستطیل کی تعریف 4 دائیں زاویوں کے ساتھ چوکور ہے۔

مستطیل کی خصوصیات یہ ہیں کہ اس کے 2 متوازی مخالف سمتیں، 2 مساوی مخالف سمتیں، 2 مساوی مخالف زاویے، 2 مساوی اخترن اور ہر لائن کے وسط میں ایک دوسرے کو کاٹتے ہیں۔

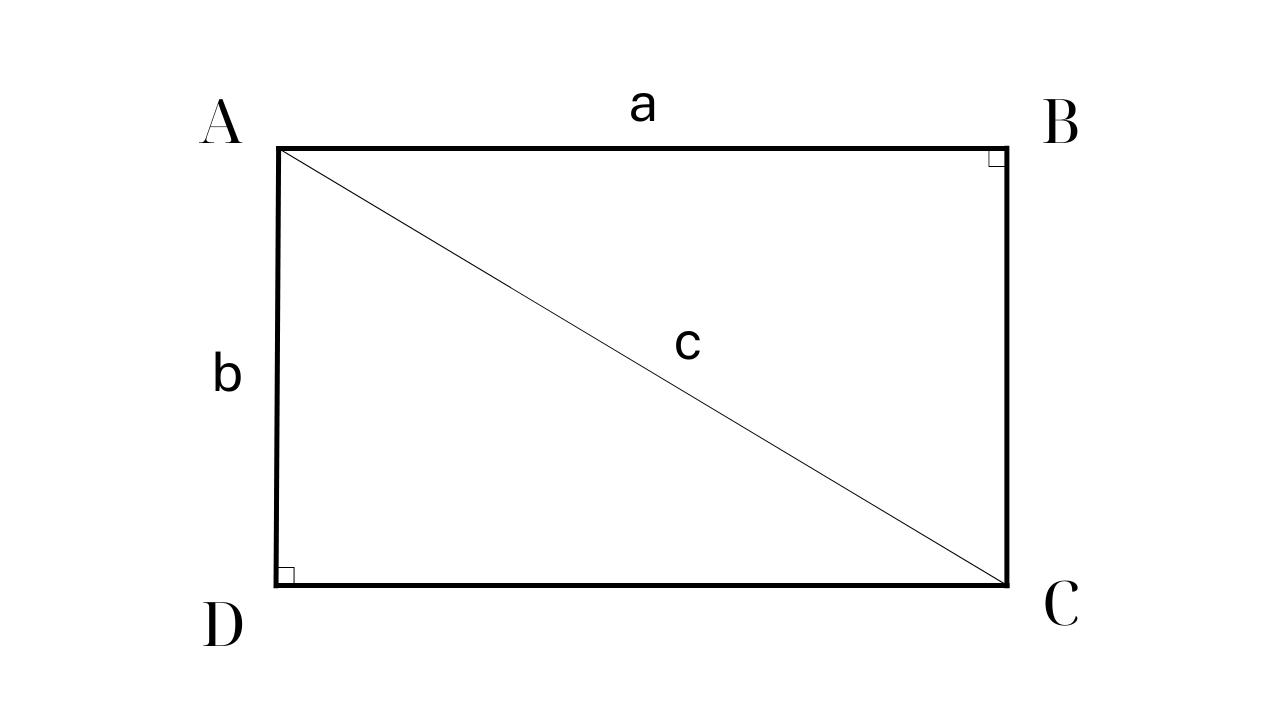
مستطیل کے رقبہ کا حساب لگانے کا فارمولا

ویتنام ایجوکیشن پبلشنگ ہاؤس کی نصابی کتاب سیریز "علم کو زندگی سے جوڑنا" کے سبق 52، ریاضی کی کتاب 3 (جلد 2) میں، مستطیل کے رقبے کو شمار کرنے کا فارمولہ لمبائی سے ضرب چوڑائی (پیمائش کی ایک ہی اکائی) ہے۔

S = axb

وہاں:

S: مستطیل کا رقبہ

a: مستطیل کی لمبائی

ب: مستطیل کی چوڑائی

مثال کے طور پر: ایک مستطیل لکڑی کے بورڈ کی چوڑائی 5cm اور لمبائی 15cm ہے۔ اس لکڑی کے تختے کے رقبے کا حساب لگائیں۔

جواب: لکڑی کے تختے کا رقبہ ہے: S = 5 x 15 = 75 ( ^cm² )

مستطیل کے رقبہ کا حساب لگانے کا فارمولا جب ایک طرف اور اخترن معلوم ہوں۔

مستطیل کے رقبے کو اس کے اخترن اور ایک طرف کے حساب سے شمار کرنے کے لیے، آپ کو بنیادی رقبہ کے فارمولے کے ساتھ پائتھاگورین تھیوریم کو جوڑنے کی ضرورت ہے۔

مرحلہ 1: باقی سائیڈ کی لمبائی کا حساب لگانے کے لیے پائتھاگورین تھیوریم کو دائیں مثلث پر لگائیں۔

مرحلہ 2: مستطیل کے رقبے کا حساب لگانے کے لیے فارمولے کا اطلاق کریں: S = axb

مثال: ایک مستطیل ABCD میں AD = 60cm اور اخترن AC = 100cm ہے۔ اے بی سی ڈی کے رقبہ کا حساب لگائیں۔

جواب:

مرحلہ 1: دائیں زاویہ مثلث میں پائتھاگورین تھیوریم کا استعمال کرتے ہوئے مستطیل ABCD کا بقیہ رخ تلاش کریں۔

اس کے مطابق: AC ² = AB ² +AD ² => AB ² = AC ² - AD ² = 10000 - 3600 = 6400 => AB = 80 (cm)

مرحلہ 2: ABCD کا رقبہ = AB x AD = 60 x 80 = 4800 ( ^cm² )

دائرہ معلوم کرتے وقت مستطیل کے رقبے کا حساب لگانے کا فارمولا

ایک مستطیل کے رقبہ کا حساب لگانے کے لیے جب فریم معلوم ہو، آپ کو دائرہ کار کے فارمولے اور بنیادی رقبہ کے فارمولے کو یکجا کرنے کی ضرورت ہے۔

مرحلہ 1: ایک مستطیل کے فریم کا حساب لگانے کے فارمولے سے P = (a+b) x 2 ہے P کے ساتھ فریم ہے، a لمبائی ہے، b مستطیل کی چوڑائی ہے، ہمارے پاس a = (P/2) - b یا b = (P/2) - a ہے۔

مرحلہ 2: a یا b تلاش کرنے کے بعد، مستطیل کے رقبے کا حساب لگانے کے لیے فارمولہ لاگو کریں: S = axb

مستطیل کو پہچاننے کے لیے نشانیاں؟

ویتنام ایجوکیشن پبلشنگ ہاؤس کے سبق 13، ریاضی 8 (جلد 1) کی نصابی کتاب کی سیریز "علم کو زندگی سے جوڑنا" کے مطابق، مستطیل کو پہچاننے کی علامات یہ ہیں:

- ایک چوکور میں 3 دائیں زاویے ہوتے ہیں (تعریف کی بنیاد پر)

- متوازی لوگرام کا 1 دائیں زاویہ ہے۔

- ایک متوازی علامت کے دو مساوی اخترن ہوتے ہیں۔

- ایک isosceles trapezoid کا ایک صحیح زاویہ ہوتا ہے۔

کیا مستطیل ایک متوازی علامت ہے؟

ویتنام ایجوکیشن پبلشنگ ہاؤس کے سبق 13، ریاضی 8 (جلد 1) کی نصابی کتاب کی سیریز "علم کو زندگی سے جوڑنا" کے مطابق، ایک مستطیل میں متوازی علامت کی تمام خصوصیات ہوتی ہیں۔ لہذا، ایک مستطیل ایک خاص متوازی گرام ہے۔

کیا ایک مستطیل ایک isosceles trapezoid ہے؟

سبق 13، ریاضی 8 (جلد 1) ویتنام ایجوکیشن پبلشنگ ہاؤس کی نصابی کتاب کی سیریز "علم کو زندگی سے جوڑنا"، مستطیل میں ایک آئوسیلس ٹراپیزائڈ کی تمام خصوصیات ہیں۔ لہذا، ایک مستطیل isosceles trapezoid کی ایک خاص شکل ہے۔

(مصنوعی)

ماخذ: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html