Vědci našli řešení klasického geometrického problému, který trval více než století

Ilustrace pro geometrický problém.

Podle deníku South China Morning Post matematik Hong Wang – v současnosti docent na Courantově institutu pro matematické vědy Newyorské univerzity (USA) – a jeho kolega Joshua Zahl (Univerzita Britské Kolumbie, Kanada) právě vyřešili jeden z nejobtížnějších geometrických problémů 20. a 21. století: Kakeyovu hypotézu v trojrozměrném prostoru.

Hong Wang se narodil ve městě Guilin (Čína), studoval na Pekingské univerzitě a poté se věnoval výuce a výzkumu v USA.

Problém vznikl v roce 1917, kdy japonský matematik Sóiči Kakeja položil otázku: „Jaká je nejmenší plocha potřebná k otočení jehly o 180 stupňů? Tento minimální prostor se nazývá „Kakeyova množina“.

Ve dvourozměrném prostoru si lze otáčení jehly za účelem vytvoření kruhu snadno představit, ale pokud je rotace flexibilnější, například když se jehlou během otáčení třese, může být plocha, kterou jehla otáčí, ještě menší.

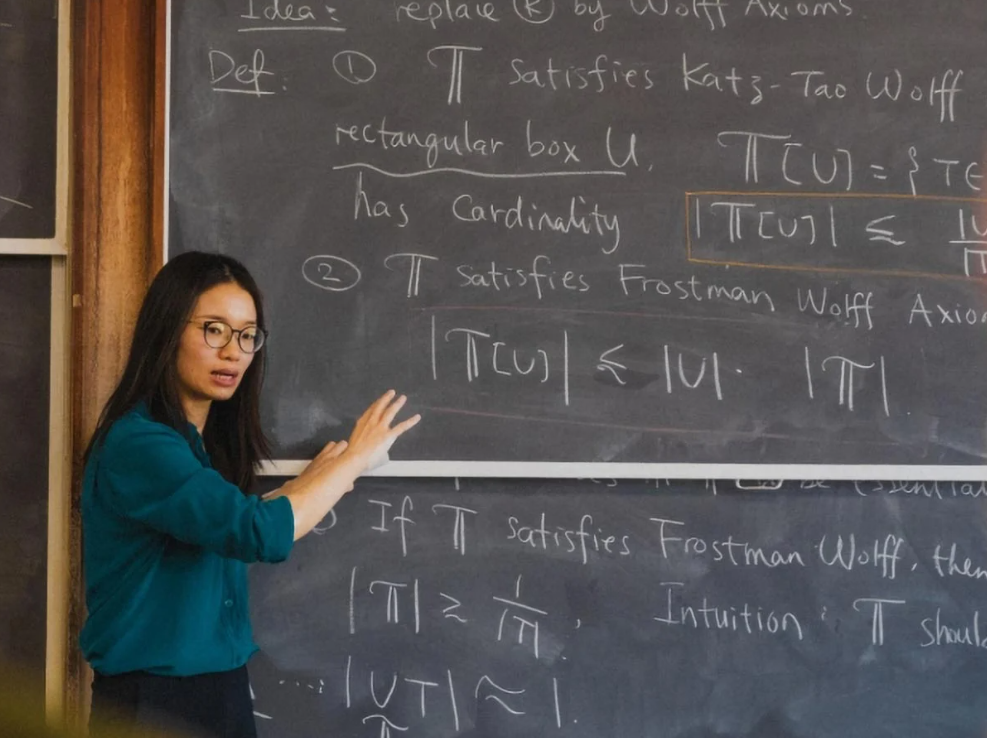
Vědci našli řešení geometrického problému, který trval více než století.

Přesunutí problému do tří rozměrů ho značně komplikuje. Kakeyova hypotéza říká, že pokud chcete otáčet jehlou všemi směry, potřebný prostor musí být dostatečně velký ve všech třech rozměrech – nelze ji vměstnat do místa, které je příliš malé nebo příliš tenké.

Ve své práci publikované na platformě arXiv Wang a Zahl dokazují, že v trojrozměrném prostoru nemusí mít oblast, ve které se jehla otáčí, jasný tvar, ale musí být dostatečně velká ve všech třech rozměrech. Díky tomu tento problém vyřešili – a to je dnes v matematice považováno za velmi důležitý objev .

Profesor Terence Tao – jeden z předních světových matematiků – to nazval „velkolepým pokrokem“. Odborníci také uvedli, že práce nejen rozšířila chápání geometrie, ale mohla by mít dopad i na mnoho oblastí, jako je zpracování obrazu, bezdrátová komunikace, informatika a kryptografie – kde je pochopení pohybů a interakcí v prostoru nesmírně důležité.

„Není to přehnané, ale jedná se o vzácné řešení, na které jsme čekali stovky let,“ řekl profesor matematiky Nets Katz, který vyučuje na Riceově univerzitě (USA).

Podle profesora Gutha Larryho, přednášejícího na Massachusettském technologickém institutu (USA), je Kakeyaova hypotéza základem „věže“ větších hypotéz v oblasti geometrie. Vyřešení této hypotézy pomůže dosáhnout a dobýt vyšší úrovně věže znalostí.

„Dříve jsem si myslel, že je to jednoduchý, základní geometrický problém, ale ve skutečnosti je tento problém příliš složitý. Tímto problémem se zabývalo mnoho velkých jmen v oblasti matematiky, ale většina z nich dosáhla jen malých výsledků, nebyla systematická a nemohla být považována za kompletní řešení,“ sdělil profesor Guth Larry.

Phuong Anh (zdroj: Science Daily, SCMP)

Zdroj: https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-hinh-hoc-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html