幾何学の問題の図解。
サウスチャイナ・モーニング・ポストによると、ニューヨーク大学クーラント数学研究所(米国)の准教授である数学者ホン・ワン氏と、同僚のジョシュア・ザール氏(カナダ、ブリティッシュコロンビア大学)が、20世紀から21世紀にかけての幾何学における最も困難な問題の一つである、三次元空間におけるカケヤ予想を解決したという。
ホン・ワン氏は桂林市(中国)で生まれ、北京大学で学んだ後、米国で教鞭をとり、研究に携わった。
この問題は1917年に日本の数学者掛谷宗一が「針を180度回転させるために必要な最小の面積はどれくらいか」という疑問を提起したことに端を発しています。その最小の空間は「掛谷集合」と呼ばれています。
2 次元空間では、針を回転させて円を描くことは簡単に視覚化できますが、回転しながら針を振るなど、回転がもっと柔軟な場合は、針が掃く領域をさらに小さくすることができます。
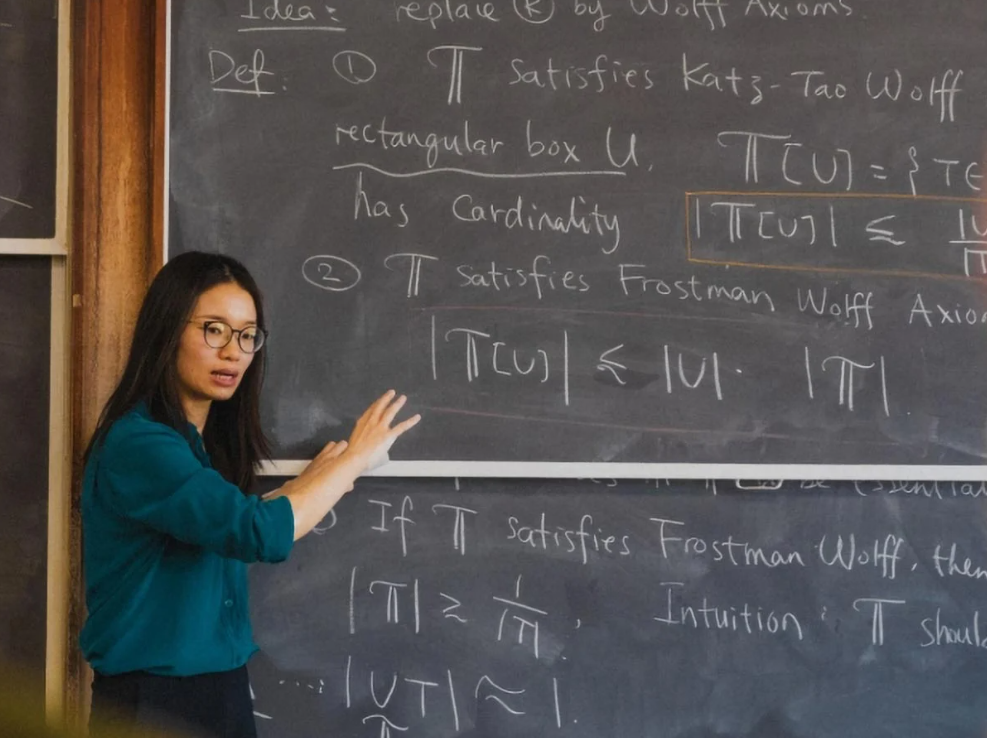
科学者たちは1世紀以上続いた幾何学の問題の解決策を発見した。
問題を3次元に移すと、はるかに複雑になります。掛谷の予想によれば、針をあらゆる方向に回転させたい場合、必要な空間は3次元すべてにおいて十分に大きくなければなりません。つまり、針を小さすぎたり薄すぎたりする場所に押し込むことはできないのです。
arXivプラットフォームに掲載された研究において、ワン氏とザール氏は、三次元空間において針が回転する領域は明確な形状を持つ必要はなく、三次元全体にわたって十分な大きさを持つ必要があることを証明しました。これにより、彼らはこの問題を解決しました。これは今日の数学における非常に重要な発見と考えられています。
世界有数の数学者、テレンス・タオ教授は、この成果を「驚異的な進歩」と評しました。専門家らはまた、この研究は幾何学の理解を深めるだけでなく、画像処理、無線通信、コンピュータサイエンス、暗号学など、空間における動きや相互作用の理解が極めて重要な多くの分野に影響を与える可能性があると述べています。
「誇張ではなく、これは私たちが何百年も待ち望んでいた稀有な解決策だ」とライス大学(米国)で教鞭をとる数学教授ネッツ・カッツ氏は語った。
マサチューセッツ工科大学(米国)の講師であるガス・ラリー教授によると、カケヤ仮説は幾何学分野におけるより大きな仮説の「塔」の基礎となるものです。この仮説を解くことで、知識の塔のより高次のレベルに近づき、それを克服する機会が得られるでしょう。
「以前はこれは単純で基本的な幾何学の問題だと思っていましたが、実際には難しすぎます。この問題は数学界の多くの著名人によって研究されてきましたが、そのほとんどは小さな成果しか得られず、体系的ではなく、完全な解決策とは言えませんでした」とガス・ラリー教授は語った。
出典: https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-hinh-hoc-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html





![[写真] 第1回政府党大会の厳粛な開会](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/13/1760337945186_ndo_br_img-0787-jpg.webp)
![[写真] ト・ラム書記長が第1回政府党大会の開会式に出席](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/13/1760321055249_ndo_br_cover-9284-jpg.webp)


































































































コメント (0)