ບັນຫາຂອງການຊອກຫາ cat ຫລັງປະຕູໄດ້

ບັນຫາຄະນິດສາດ ມ5 ຂໍໃຫ້ຜູ້ອ່ານຄິດໄລ່ຈໍານວນປະຕູທີ່ຈະເປີດເພື່ອຊອກຫາແມວ, ຮູ້ວ່າຫຼັງຈາກແຕ່ລະເປີດປະຕູເປົ່າ, ແມວຈະຍ້າຍໄປປະຕູອື່ນ.

ຫົວຂໍ້:

ຫ້ອງໂຖງຊື່ມີຫ້າປະຕູຢູ່ຂ້າງຫນຶ່ງ. ຫລັງປະຕູຫນຶ່ງແມ່ນແມວ. ວຽກງານຂອງທ່ານແມ່ນເພື່ອຊອກຫາ cat ໄດ້ໂດຍການເປີດປະຕູທີ່ຖືກຕ້ອງ. ທ່ານສາມາດເປີດປະຕູດຽວໃນແຕ່ລະມື້. ຖ້າແມວຢູ່ທີ່ນັ້ນ, ເຈົ້າຊະນະ.

ຖ້າແມວບໍ່ຢູ່, ປະຕູຈະປິດ, ແລະເຈົ້າຕ້ອງລໍຖ້າຈົນກ່ວາມື້ຕໍ່ມາກ່ອນທີ່ທ່ານຈະສາມາດເປີດປະຕູໄດ້. ແມວແມ່ນເຄື່ອນຍ້າຍຢ່າງຕໍ່ເນື່ອງ, ແລະໃນແຕ່ລະຄືນມັນຍ້າຍໄປນັ່ງຢູ່ຫລັງປະຕູທີ່ແຕກຕ່າງກັນ. ປະຕູທີ່ມັນຍ້າຍໄປຈະເປັນປະຕູທາງຊ້າຍຫຼືຂວາຂອງບ່ອນທີ່ມັນຢູ່ໃນປັດຈຸບັນ.

ເຈົ້າຕ້ອງແນ່ໃຈວ່າເຈົ້າພົບແມວຈັກມື້?

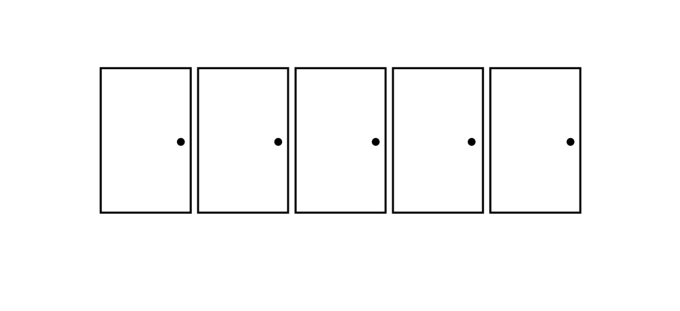
ບັນຫາແມ່ນຂໍໃຫ້ເຈົ້າຊອກຫາຍຸດທະສາດທີ່ຮັບປະກັນວ່າເຈົ້າຈະຈັບແມວໃນຈໍານວນມື້ຄົງທີ່, ບໍ່ວ່າຈະເປັນປະຕູໃດທີ່ມັນຈະເລີ່ມຕົ້ນຢູ່ຫລັງແລະບ່ອນທີ່ມັນຍ້າຍໄປໃນຕອນກາງຄືນ. ສິ່ງສໍາຄັນໃນການແກ້ໄຂບັນຫາແມ່ນເລີ່ມຕົ້ນດ້ວຍຈໍານວນປະຕູນ້ອຍລົງ, ຊອກຫາຮູບແບບ, ແລະຫຼັງຈາກນັ້ນເພີ່ມຈໍານວນປະຕູ.

ໃຫ້ເລີ່ມຕົ້ນດ້ວຍກໍລະນີທີ່ມີພຽງແຕ່ສາມປະຕູ. ຖ້າເຈົ້າເປີດປະຕູກາງສອງມື້ຕິດຕໍ່ກັນ, ເຈົ້າຮັບປະກັນທີ່ຈະຈັບແມວ, ເພາະວ່າຖ້າແມວບໍ່ຢູ່ຫລັງປະຕູກາງໃນມື້ຫນຶ່ງ, ມັນຕ້ອງຢູ່ຫລັງຫນຶ່ງຂອງສອງປະຕູ. ແລະຖ້າມັນຢູ່ຫລັງປະຕູສຸດທ້າຍໃນມື້ຫນຶ່ງ, ມັນບໍ່ມີທາງເລືອກນອກເຫນືອຈາກການຍ້າຍໄປປະຕູກາງໃນມື້ທີສອງ.

ຖ້າມີສີ່ປະຕູ, ເຈົ້າສາມາດຈັບແມວໄດ້ໃນສີ່ມື້. ທ່ານສາມາດຊອກຫາຄໍາອະທິບາຍໃນຄໍາຕອບຂ້າງລຸ່ມນີ້, ແຕ່ກ່ອນນັ້ນ, ພະຍາຍາມອະທິບາຍຕົວເອງ. ຈືຂໍ້ມູນການ, ແມວພຽງແຕ່ຍ້າຍໄປຫາປະຕູທັນທີໄປທາງຂວາຫຼືຊ້າຍຂອງມັນແລະສາມາດກັບຄືນໄປຫາປະຕູທີ່ມັນຢູ່ຫລັງກ່ອນ. ເຊື່ອວ່າເຈົ້າຈະມີຄວາມສຸກເມື່ອພົບຄຳອະທິບາຍ.

>>> ຕອບ

Vo Quoc Ba Can

ຄູຄະນິດສາດ, ໂຮງຮຽນ Archimedes ຮ່າໂນ້ຍ

ແຫຼ່ງທີ່ມາ