Será que os alunos estão aprendendo matemática sem pensar?

Existe algum tipo de matemática "não racional"?

O Dr. Nguyen Phi Le (Escola de Tecnologia da Informação e Comunicação, Universidade de Ciência e Tecnologia de Hanói ) já foi um bom aluno de matemática, tendo conquistado uma medalha de prata na competição internacional de matemática da IMO em 2000, sem precisar fazer muitas aulas extras. Portanto, quando seu filho ainda estava no ensino fundamental, o Dr. Le não achava que ele precisasse de aulas extras de matemática em geral, e de "matemática racional" em particular, embora na época muitos centros de reforço escolar já estivessem anunciando o ensino de "matemática racional". No entanto, quando seu filho estava na 5ª série e, posteriormente, prestou o vestibular para o ensino médio, o Dr. Le se viu obrigado a matriculá-lo em aulas extras de matemática, pois somente assim ele conseguiria passar no exame de admissão para escolas especializadas e turmas seletivas.

Muitos pais permitem que seus filhos aprendam matemática desde cedo, na esperança de que eles se saiam bem na matéria.

Por exemplo, recentemente, após o exame de admissão para o 10º ano com especialização em matemática na Escola de Ciências Naturais da Universidade de Ciências Naturais da Universidade Nacional de Hanói, professores e alunos discutiram bastante sobre uma questão de geometria. Um bom professor de geometria disse que havia dedicado de três a quatro horas para resolver essa questão. No entanto, um aluno do 9º ano teve que resolvê-la em pouco tempo. Nesse exame, se um aluno não tivesse feito provas anteriores e nunca tivesse resolvido questões semelhantes, certamente não conseguiria. Mesmo um aluno com excelente capacidade de raciocínio não conseguiria.

"Imagine fazer uma prova muito difícil, com um formato incomum, em pouco tempo. Para fazer uma prova assim, os alunos precisam de muito tempo", explicou o Dr. Le.

A Dra. Le também disse que, ao ver seu filho fazendo muitas aulas extras, aconselhou-o a dedicar mais tempo aos estudos individuais, pois somente assim o cérebro do aluno teria tempo para absorver o conhecimento, ajudando-o a se tornar autossuficiente e capaz de ser independente mais tarde ao enfrentar problemas que precisassem ser resolvidos. No entanto, seu filho não se sentiu seguro, pois temia não conseguir competir com seus amigos em uma corrida onde a força pertencia aos alunos que se dedicavam aos cursos preparatórios para os exames.

Segundo o Professor Le Anh Vinh, Diretor do Instituto Vietnamita de Ciências da Educação , muitos matemáticos sentem aversão quando alguém diz "matemática que exige raciocínio". Isso porque, para eles, significa que existe uma "matemática que não exige raciocínio"? Mas a realidade é que o método de ensino atual apresenta muitas formas de ensinar matemática que não incentivam o raciocínio, focando-se apenas no cálculo. Em sala de aula, os professores costumam ensinar os alunos a resolver exercícios seguindo modelos (o que muitas vezes é chamado de matemática por forma). Com esse método, quando os alunos já resolveram um determinado problema, ao se depararem com ele novamente, geralmente resolvem o exercício muito rapidamente, sem pensar em nada.

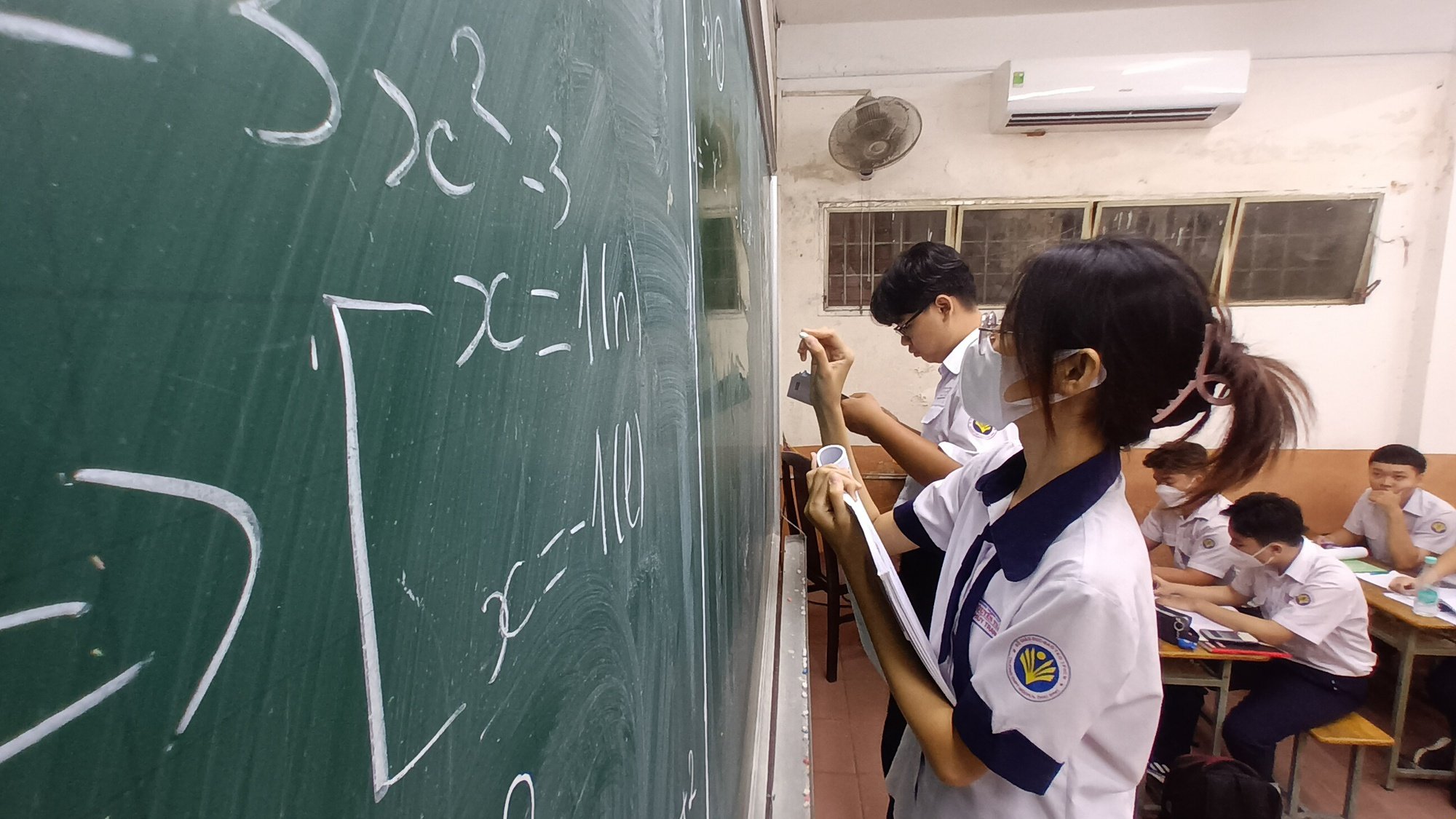
O novo programa de educação geral concentra-se na matemática conectada à prática, à aplicação, à resolução da questão de para que serve a matemática, e não apenas na realização de exercícios.

QUANDO APRENDER MATEMÁTICA DEIXA DE SER A NATUREZA DO APRENDER MATEMÁTICA

Segundo a Dra. Vu Thi Ngoc Ha, do Instituto de Matemática Aplicada e Informática da Universidade de Ciência e Tecnologia de Hanói, todas as disciplinas científicas promovem o desenvolvimento e o aperfeiçoamento do pensamento em cada criança, o que é chamado de "diversidade de campos fundamentais", e não apenas o aprendizado da matemática que desenvolve o raciocínio.

Em matemática, porém, os problemas estão sempre relacionados à realidade. Para ser aprovado, o aluno deve percorrer as etapas de construção do problema com base na análise das leis dos fenômenos naturais e, em seguida, usar o raciocínio lógico, o pensamento criativo etc. para resolvê-lo. Nesse processo, a imaginação e o pensamento crítico são estimulados para a resolução do problema.

"A matemática em si parece ser a disciplina que estimula o pensamento mais perfeito. Portanto, o surgimento de centros de 'pensamento matemático' é compreensível na situação atual, em que temos que enfrentar a tarefa de dominar um determinado módulo de conhecimento de cada disciplina em um tempo muito curto, não apenas matemática, para prestar exames. A partir daí, aprender matemática deixa de ser fiel à sua essência", comentou o Dr. Ngoc Ha.

O professor Le Anh Vinh disse que, a princípio, também tinha aversão à expressão "matemática que estimula o pensamento". Após pesquisas posteriores, descobriu que o ensino da matemática sem o devido pensamento ainda é bastante popular. O professor Vinh comentou: "Se dissermos que ensinamos matemática aqui, e não matemática sem pensamento, soa muito pesado. Portanto, quando alguém ou alguma instituição se apresenta como ensinando matemática que estimula o pensamento, significa que está ensinando matemática no verdadeiro sentido da palavra. Assim, 'matemática que estimula o pensamento' surge do desejo de ensinar matemática para que os alunos reflitam e sejam capazes de aplicá-la na vida, e não apenas para que os alunos obtenham notas altas nas provas. Os pais também devem levar isso em consideração, pois quando se apresentam dessa forma, significa que não estão ensinando os alunos a aprender matemática para se saírem bem nas provas, mas sim a pensar".

NECESSÁRIO PARA A INOVAÇÃO EM EXAMES

A Dra. Ngoc Ha acredita que, para que o aprendizado da matemática retorne à sua verdadeira natureza, os alunos precisam "aprender devagar", pois o "aprendizado lento" é a maneira mais eficaz de estimular o desenvolvimento do pensamento de cada criança.

Ao se depararem com um problema, os alunos precisam de tempo (muito tempo) para identificar fenômenos naturais, a partir daí buscar grandezas e regras para encontrar a relação entre elas por meio de expressões, e então procurar ferramentas metodológicas para resolver o problema. Assim, construir um programa chamado "pensamento matemático" é muito difícil. Mas ensinar é ainda mais difícil, porque além de conduzir "devagar, muito devagar", o professor precisa ter um conhecimento geral amplo e de alto nível. O ensino deve ser flexível e adequado às qualidades e habilidades de cada aluno. Isso é muito difícil de fazer quando se enfrenta a pressão do desempenho acadêmico, a necessidade de prêmios, notas e as expectativas dos pais, tudo isso no tempo da criança...

Ensine os ALUNOS a pensar, não a calcular.

O professor Le Anh Vinh costuma dizer, em tom de brincadeira, aos professores de matemática: ensinar os alunos a pensar por 10 minutos é mais difícil do que ensiná-los a sentar e calcular por uma hora. Se ir à escola se resume a receber uma folha de exercícios e sentar para calcular o mais rápido e corretamente possível, então, ao final da aula, nada restará na mente dos alunos. Ao se depararem com novas situações, os alunos não conseguem pensar, não conseguem aplicar o que aprenderam para resolver problemas. No entanto, esse é um problema sistêmico, que se manifesta na narrativa de provas, testes e tipos de exercícios, fazendo com que as pessoas ignorem todas as etapas que desenvolvem o pensamento, focando apenas em ensinar os alunos a calcular e fazer exercícios.

Em particular, ensinar matemática como ensinar a pensar exige a sincronização de todo um sistema: programa, livros didáticos, tempo a cada hora e a cada minuto, cada disciplina, sistema de avaliação, psicologia social...

Alunos do 9º ano na sala de provas de matemática do recente exame de admissão para o 10º ano, na cidade de Ho Chi Minh. A prova de matemática continha muitos problemas práticos.

Segundo o professor Vinh, o novo programa de educação geral foca na conexão da matemática com a realidade, com a aplicação prática e na busca de respostas para a questão de por que aprendemos matemática, e não apenas por meio da prática de exercícios.

A Dra. Phi Le afirmou que apoia os alunos que fazem aulas extras em matérias de seu interesse e nas quais são capazes, mas de uma forma que aprimore sua criatividade e capacidade de raciocínio. Fazer aulas extras com foco na preparação para exames, como acontece atualmente, não é muito benéfico para os alunos. "O problema é que a forma como as questões são elaboradas hoje faz com que os alunos que nunca estudaram os tipos de questões da prova se tornem 'perdedores'. O ambiente atual de exames cria uma competição desigual entre os alunos que aprendem a 'pensar' e os alunos que aprendem a se preparar para as provas. Pensar exige muito tempo e envolve aceitar o risco de não saber responder a muitos tipos de questões. Essa é a 'motivação' que faz com que os alunos sejam 'forçados' a fazer aulas extras."

Então, como os exames devem ser elaborados para desenvolver o pensamento dos alunos? As questões dos exames não devem ser capciosas, devem ser consistentes com o conteúdo ensinado nas escolas regulares e também devem identificar alunos com bom raciocínio”, disse o Dr. Phi Le.

Link da fonte: https://thanhnien.vn/phai-chang-hoc-sinh-dang-hoc-toan-khong-tu-duy-185230609045433219.htm