2025'te Hanoi'deki 10. sınıf giriş sınavı için önerilen matematik cevapları

Hanoi Eğitim ve Öğretim Dairesi, 2025 yılı 10. sınıf giriş sınavı için 7 dersten örnek soruları duyurdu. Bu 7 ders arasında edebiyat, matematik, yabancı diller, fen bilimleri, tarih ve coğrafya, yurttaşlık bilgisi ve bilgi teknolojisi yer alıyor.

Hanoi'de 2025 eğitim öğretim yılında yapılacak 10. sınıf giriş sınavı için örnek matematik sınavı (Ekran Görüntüsü).

Matematikte sınav bilgisi 3 bölümden oluşmaktadır: Sayılar ve cebir 4,5 puan, geometri ve ölçme 4 puan, istatistik ve olasılık 1,5 puandır.

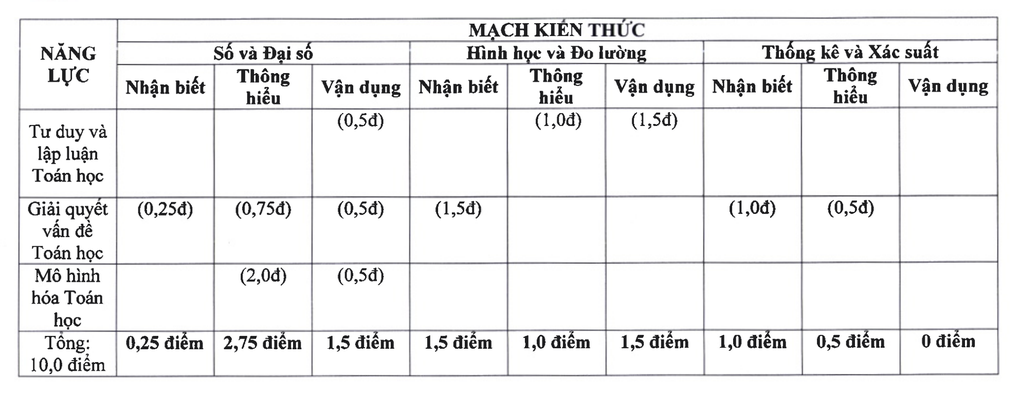
2025 yılında Hanoi'de yapılacak 10. sınıf giriş sınavı için matematik bilgi devresi (Ekran Görüntüsü).

>> 2025 yılında Hanoi'de 10. sınıf için matematik sınavına yönelik önerilen ayrıntılı cevapları tuyensinh247 mesleki bölüm öğretmenlerinden BURADAN görün

Matematik çizim testi incelemesi

Öğretmen Do Van Bao’ya göre sınavın genel yapısı şu şekilde düzenlenmiştir:

Bölüm I: (1,5 puan) İstatistik ve olasılıkla ilgili 2 sorudan oluşmaktadır.

- Veri istatistikleri, grafikler

- Olasılık

Bölüm II: (1,5 puan) Önceki yıllardaki sınavlardaki Soru I'e benzer cebirsel ifadelerle ilgili 3 sorudan oluşmaktadır.

- İfade değerlerini hesaplayın, öğrencilerin temel becerilerini test edin

- İfadeyi basitleştirin

- Öğrencileri farklılaştırmak için ek sorular

Ders III: (2,5 puan) Denklem sistemleri ve ikinci dereceden denklemlerle ilgili 3 soru içerir.

- Cümle 1,2: Denklem sistemleri kurarak gerçek yaşam problemlerini çözün, denklemler kurun

- Soru 3 İkinci dereceden denklem

Ders IV. Geometri

- Uzaysal geometri

- Çemberlerle ilgili problemler

Ders V. Gerçek dünya faktörleriyle ilgili geometrik ekstremumlara ilişkin ileri problemler.

Toplam puan: 10 puan, cebirden, geometriye, pratik uygulamalara kadar temel ve ileri bilgi bölümleri arasında eşit olarak dağıtılır.

Bilgi içeriğine ilişkin yorumlar

Cebir Bölümü: İfadeli hesaplamalar, ikinci dereceden denklemler ve uygulamalar gibi temel içerikleri içerir. Örnek testin yeni noktası, gerçek hayattaki problemlerden yararlanan ve öğrencilerin günlük hayattaki problemlere Matematik yoluyla yaklaşmalarına yardımcı olan birçok soru içermesidir.

Geometri Bölümü: Düzlem geometrisi, daireler ve iç teğet dörtgenlerle ilgili problemler, uzaysal geometri, geometrik ispatlar ve pratikte geometrik uygulamalar gibi bilindik konuları içerir. Sınav, öğrencilerin iyi uzaysal düşünme ve geometrik teoriyi pratik problemlere uygulama becerisine sahip olmalarını gerektirir.

İstatistik ve Olasılık bölümü: Ders I'de yer alan, önceki yıllara göre yeni içerikli, öğrencilerin grafikleri analiz etmelerini ve olasılık hesaplamalarını gerektiren, pratik uygulama ağırlıklı ve yeni ders programlarında sıkça yer alan bir bölümdür.

Zorluk hakkındaki yorumlar

Temel ve Orta Seviye: İfadeleri değerlendirme, ikinci dereceden denklemleri çözme ve olasılık hesaplama ile ilgili soruların tamamı temel ve orta seviyededir. Öğrencilerin bu soruları çözebilmeleri için temel konulara hakim olmaları yeterlidir.

İleri Seviye: Geometrik ispatlar, uzaysal geometri içeren pratik problemler ve banka faiz hesaplamaları üzerine sorular, öğrencilerin iyi mantıksal düşünme ve bilgiyi pratikte uygulama becerisine sahip olmalarını gerektirir. Bu sorular, ortalama öğrenme yeteneğine sahip öğrenciler için genellikle zorlayıcı olacaktır.

Hanoi'nin örnek sınavı, öğrencilerin bilgi ve becerilerini, özellikle bunları pratikte uygulama yeteneklerini kapsamlı bir şekilde test etmeye odaklanarak yeni Genel Eğitim programını yakından takip edecek şekilde tasarlanmıştır.

Sınav, geleneksel yapının %60-70'ini korurken, içerik ve soru hazırlama yöntemlerinde yenilikler içeriyor ve öğrencilerin daha kapsamlı değerlendirilmesine yardımcı oluyor.

Sınavın zorluk derecesi orta düzeyde olup, iyi öğrencileri seçmek için belirgin bir farklılaşma bulunmaktadır.

Önceki yıllarda, sınavlar genellikle saf cebir ve geometri sorularıyla iyi ve ortalama öğrenciler arasında net bir ayrım yapıyordu. Örnek sınav, öğrencilerin yalnızca bilgi sahibi olmalarını değil, aynı zamanda bu bilgiyi belirli durumlara nasıl uygulayacaklarını da anlamalarını gerektiren pratik unsurlar içeriyordu.

Bu yılki örnek sınavın yapısı, derslerdeki bilgi içeriğinin sınıflandırılması, soru tiplerinin iç içe geçmesi ve özellikle uygulamalı problemlerin artmasıyla önceki yıllara kıyasla önemli ölçüde yenilendi. Bu, yeni eğitim programının öğrencilerin bilgiyi uygulama ve düşünceyi sentezleme becerilerini test etmeye daha fazla odaklanmasını yansıtıyor.

Sınavda başarılı olmak için 9. sınıf öğrencilerinin şunlara ihtiyacı vardır:

Örnek sınavla aynı yapı ve içerikte olan 10. sınıf giriş sınavına iyi bir şekilde hazırlanmak için 9. sınıf öğrencilerinin şu adımları izlemesi gerekiyor:

1. Temelleri kavrayın

Cebir: 9. sınıf programındaki temel bilgilere hakim olmanız gerekir, bunlar şunlardır:

Birinci ve ikinci dereceden denklemler, çözümleri ve özellikleri.

Düzlem ve katı geometriye ilişkin formüller, özellikle üçgenler, daireler ve temel geometrik şekillerle ilgili teoremler.

Denklemler kurarak sorunları çözün

Geometri: Bilgi, çemberler, iç teğet dörtgenler ve özellikleri hakkında teoremler, benzer üçgenlerin ispatı ve benzer üçgenlerin özelliklerinin uygulanması,...

İstatistik ve Olasılık: Histogram, frekans tabloları, basit olasılık hesaplamaları gibi temel istatistik kavramlarına aşina olmak gerekir, çünkü bunlar sınavda çıkabilecek bölümlerdir.

2. Gerçek matematik problemlerini çözme pratiği yapın

Uygulamalı Matematik: Öğrencilerin gerçek yaşamla ilgili problemlerle, denklemler kurarak problem çözme, denklem sistemleri kurma, üretim ve yönetim problemleri çözme veya uzaysal geometriyle ilgili problemlerle pratik yapmaları gerekmektedir.

Bilgiyi gerçeğe uygulama: Hacim ve alan ölçümü ve hesaplamasıyla ilgili pratik problemler. Bu, öğrencilerin matematiği hayata nasıl uygulayacaklarını daha iyi anlamalarına yardımcı olur.

3. Mantıksal düşünme ve analitik becerilerinizi geliştirin

Matematiksel İspat: Geometrik ve cebirsel ispat problemlerinde pratiği güçlendirin. Özellikle, düzlem veya uzaysal geometrideki elemanlar arasındaki ilişkilerin ispatını gerektiren problemler, mantıksal düşünmeyi geliştirmek için gereklidir.

Problemleri analiz edin ve çözün: Soruları analiz etme alıştırması yapın ve çözmeye başlamadan önce her sorunun gerekliliklerini anlayın. Bu, kafa karışıklığını önlemeye ve sınav sürecinde doğruluğu artırmaya yardımcı olur.

Kaynak: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm