Wissenschaftler finden Lösung für klassisches Geometrieproblem, das mehr als ein Jahrhundert lang Bestand hatte

Illustration für ein Geometrieproblem.

Laut der South China Morning Post haben der Mathematiker Hong Wang – derzeit außerordentlicher Professor am Courant Institute for Mathematical Sciences der New York University (USA) – und sein Kollege Joshua Zahl (University of British Columbia, Kanada) gerade eines der schwierigsten Geometrieprobleme des 20. und 21. Jahrhunderts gelöst: die Kakeya-Vermutung im dreidimensionalen Raum.

Hong Wang wurde in der Stadt Guilin (China) geboren und studierte an der Peking-Universität, bevor er in den USA lehrte und forschte.

Das Problem entstand im Jahr 1917, als der japanische Mathematiker Sōichi Kakeya die Frage stellte: „Was ist die kleinste Fläche, die benötigt wird, um eine Nadel um 180 Grad zu drehen?“ Dieser minimale Raum wird als „Kakeya-Menge“ bezeichnet.

Im zweidimensionalen Raum lässt sich das Drehen der Nadel zur Bildung eines Kreises leicht visualisieren. Wenn die Drehung jedoch flexibler ist, beispielsweise durch Schütteln der Nadel während der Drehung, kann der Bereich, den die Nadel überstreicht, noch kleiner sein.

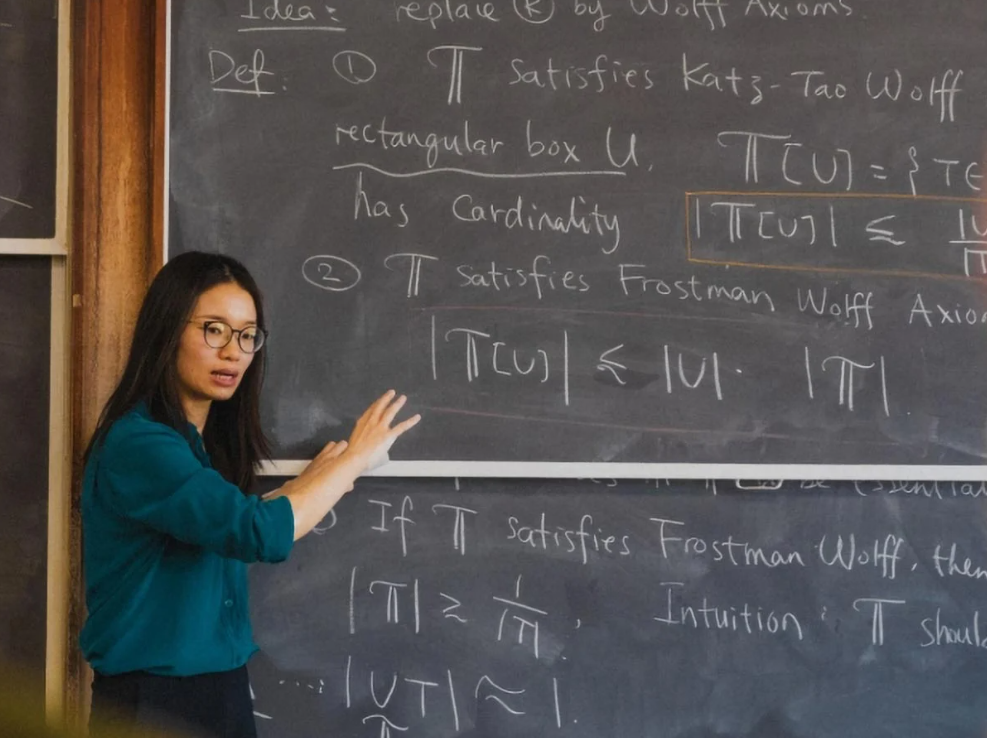
Wissenschaftler finden Lösung für ein Geometrieproblem, das mehr als ein Jahrhundert gedauert hat.

Die Übertragung des Problems in drei Dimensionen macht es noch komplizierter. Kakeyas Vermutung besagt, dass, wenn man die Nadel in alle Richtungen drehen will, der benötigte Raum in allen drei Dimensionen groß genug sein muss – man kann sie nicht in eine zu kleine oder zu schmale Stelle quetschen.

In ihrer auf der Plattform arXiv veröffentlichten Arbeit beweisen Wang und Zahl, dass der Bereich, in dem sich die Nadel dreht, im dreidimensionalen Raum keine klare Form haben muss, aber dennoch in allen drei Dimensionen groß genug sein muss. Damit lösten sie dieses Problem – eine Entdeckung , die heute in der Mathematik als sehr wichtig gilt.

Professor Terence Tao, einer der weltweit führenden Mathematiker, bezeichnete dies als „spektakulären Fortschritt“. Experten sagten zudem, die Arbeit habe nicht nur das Verständnis der Geometrie erweitert, sondern könne auch viele Bereiche wie Bildverarbeitung, drahtlose Kommunikation, Informatik und Kryptographie beeinflussen, in denen das Verständnis von Bewegungen und Interaktionen im Raum von größter Bedeutung sei.

„Es ist keine Übertreibung, aber dies ist eine seltene Lösung, auf die wir Hunderte von Jahren gewartet haben“, sagte Professor für Mathematiknetze Katz, der an der Rice University (USA) lehrt.

Laut Professor Guth Larry, Dozent am Massachusetts Institute of Technology (USA), ist die Kakeya-Hypothese die Grundlage eines „Turms“ größerer Hypothesen im Bereich der Geometrie. Die Lösung dieser Hypothese wird dazu beitragen, dass die höheren Ebenen des Wissensturms erreicht und erobert werden können.

„Früher dachte ich, dies sei ein einfaches, grundlegendes Geometrieproblem, aber in Wirklichkeit ist es zu schwierig. Viele große Namen auf dem Gebiet der Mathematik haben sich mit diesem Problem beschäftigt, aber die meisten von ihnen erzielten nur kleine Ergebnisse, waren nicht systematisch und konnten nicht als vollständige Lösung betrachtet werden“, erklärte Professor Guth Larry.

Phuong Anh (Quelle: Science Daily, SCMP)

Quelle: https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-hinh-hoc-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html