Μαθαίνουν οι μαθητές «μαθηματικά χωρίς να σκέφτονται»;

ΥΠΑΡΧΕΙ ΚΑΠΟΙΟ ΕΙΔΟΣ «ΜΗ ΣΚΕΨΗΣ» ΜΑΘΗΜΑΤΙΚΩΝ;

Ο Δρ. Nguyen Phi Le (Σχολή Τεχνολογίας Πληροφορικής και Επικοινωνιών, Πανεπιστήμιο Επιστήμης και Τεχνολογίας του Ανόι ) ήταν κάποτε καλός μαθητής στα μαθηματικά, κερδίζοντας ένα ασημένιο μετάλλιο στον διεθνή διαγωνισμό μαθηματικών του 2000 κατά την IMO χωρίς να χρειαστεί να παρακολουθήσει πολλά επιπλέον μαθήματα. Επομένως, όταν το παιδί του ήταν ακόμα στο δημοτικό σχολείο, ο Δρ. Le δεν πίστευε ότι το παιδί του χρειαζόταν να παρακολουθήσει επιπλέον μαθήματα μαθηματικών γενικά και «μαθηματικών σκέψης» ειδικότερα, παρόλο που εκείνη την εποχή στην αγορά των ιδιαίτερων μαθημάτων είχαν αρχίσει να εμφανίζονται πολλά κέντρα που διαφημίζουν τη διδασκαλία «μαθηματικών σκέψης». Ωστόσο, όταν το παιδί του ήταν στην 5η τάξη και αργότερα έδωσε εισαγωγικές εξετάσεις για την 10η τάξη, ο Δρ. Le αναγκάστηκε να αφήσει το παιδί του να παρακολουθήσει επιπλέον μαθήματα μαθηματικών, επειδή μόνο τότε μπορούσε να περάσει τις εισαγωγικές εξετάσεις σε εξειδικευμένα σχολεία και επιλεγμένες τάξεις.

Πολλοί γονείς αφήνουν τα παιδιά τους να μαθαίνουν μαθηματικά από μικρή ηλικία με την ελπίδα ότι τα παιδιά τους θα τα πάνε καλά στα μαθηματικά.

«Για παράδειγμα, πρόσφατα, μετά τις εισαγωγικές εξετάσεις για την δευτέρα τάξη με εξειδίκευση στα μαθηματικά στο Λύκειο Φυσικών Επιστημών του Πανεπιστημίου Φυσικών Επιστημών του Εθνικού Πανεπιστημίου του Ανόι, καθηγητές και μαθητές συζήτησαν πολύ για ένα θέμα γεωμετρίας. Ένας καλός καθηγητής με εξειδίκευση στη γεωμετρία είπε ότι είχε καθίσει και είχε απαντήσει σε αυτό το ερώτημα για 3-4 ώρες. Ωστόσο, ένας μαθητής της δευτέρας τάξης έπρεπε να το απαντήσει σε σύντομο χρονικό διάστημα. Με αυτήν την εξέταση, αν ένας μαθητής δεν πήγαινε σε εξετάσεις εξάσκησης και δεν είχε απαντήσει ποτέ σε παρόμοιου είδους ερωτήσεις, σίγουρα δεν μπορούσε να το απαντήσει. Ακόμα και ένας μαθητής με πολύ καλές δεξιότητες σκέψης δεν θα μπορούσε...»

«Κάντε ένα πολύ δύσκολο τεστ με μια παράξενη μορφή σε σύντομο χρονικό διάστημα. Για να κάνουν ένα τέτοιο τεστ, οι μαθητές χρειάζονται πολύ χρόνο», μοιράστηκε ο Δρ. Le.

Η Δρ. Λε είπε επίσης ότι όταν έβλεπε το παιδί της να παρακολουθεί πάρα πολλά επιπλέον μαθήματα, το συμβούλευε να αφιερώνει περισσότερο χρόνο μελετώντας μόνο του, επειδή μόνο τότε ο εγκέφαλος του μαθητή θα είχε χρόνο να απορροφήσει τη γνώση, βοηθώντας τον μαθητή να είναι αυτοδύναμος και να έχει την ικανότητα να είναι ανεξάρτητος αργότερα όταν αντιμετωπίζει προβλήματα που πρέπει να λυθούν. Ωστόσο, το παιδί της δεν ήταν καθησυχασμένο, επειδή φοβόταν ότι δεν θα μπορούσε να ανταγωνιστεί τους φίλους του σε έναν αγώνα όπου η δύναμη ανήκε σε μαθητές που δούλεψαν σκληρά στα μαθήματα προετοιμασίας για τις εξετάσεις.

Σύμφωνα με τον καθηγητή Le Anh Vinh, Διευθυντή του Ινστιτούτου Εκπαιδευτικών Επιστημών του Βιετνάμ, πολλοί μαθηματικοί είναι αλλεργικοί όταν κάποιος λέει «σκεπτόμενα μαθηματικά». Γιατί λέγοντας αυτό σημαίνει ότι υπάρχουν «μη-σκεπτόμενα μαθηματικά»; Αλλά η πραγματικότητα είναι ότι η τρέχουσα μέθοδος διδασκαλίας έχει πολλούς τρόπους διδασκαλίας των μαθηματικών που δεν διδάσκουν τη σκέψη, αλλά μόνο μαθαίνουν να υπολογίζουν. Όταν βρίσκονται στην τάξη, οι εκπαιδευτικοί συχνά διδάσκουν κυρίως στους μαθητές να κάνουν ασκήσεις σύμφωνα με μοντέλα (συχνά ονομάζονται μαθηματικά με βάση τη μορφή). Με αυτήν τη μέθοδο διδασκαλίας, όταν οι μαθητές έχουν λύσει ένα συγκεκριμένο είδος μαθηματικών, όταν το συναντούν ξανά, συχνά κάνουν την άσκηση πολύ γρήγορα, χωρίς να χρειάζεται να σκεφτούν καθόλου.

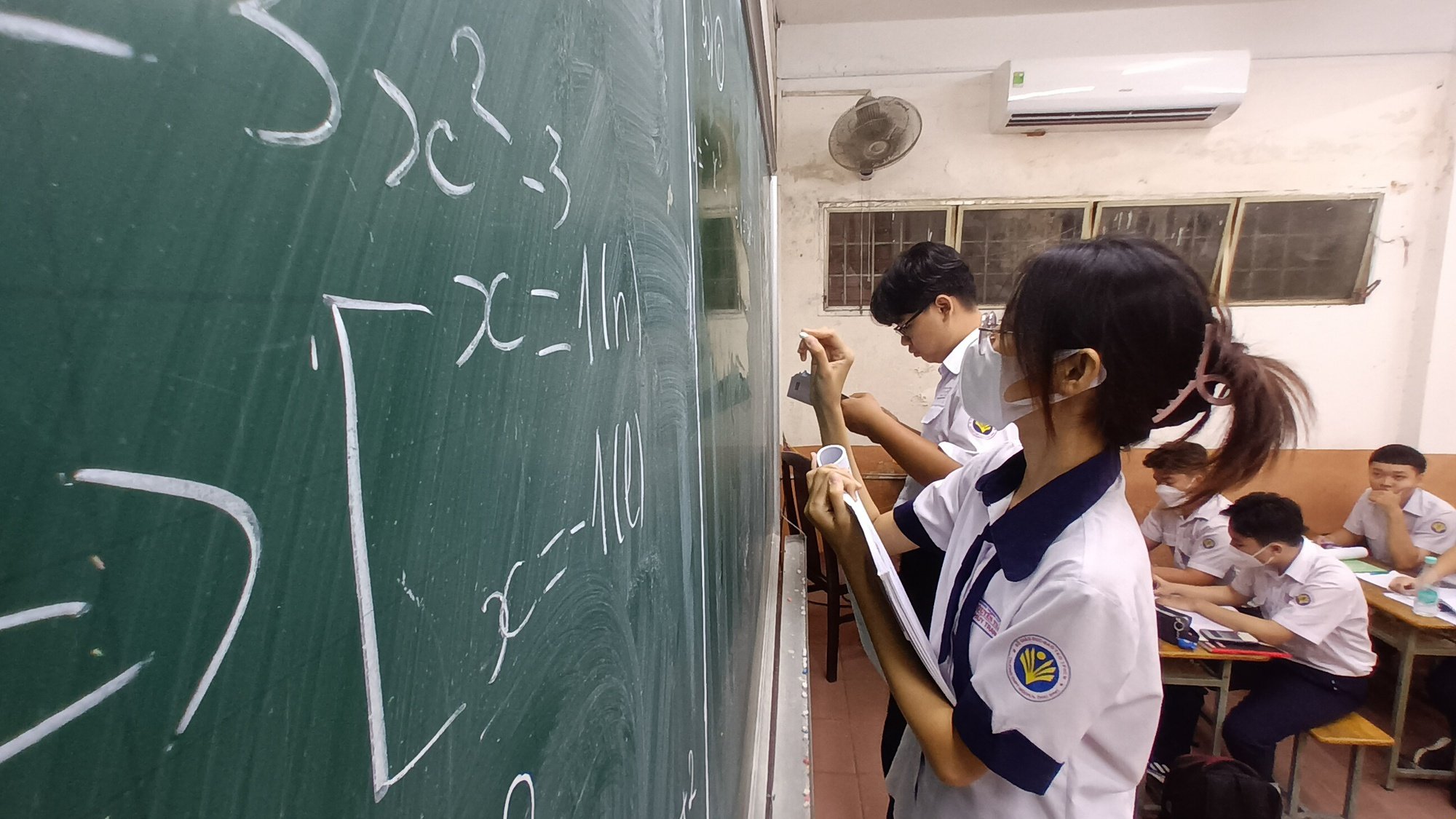
Το νέο πρόγραμμα γενικής εκπαίδευσης επικεντρώνεται στα μαθηματικά που συνδέονται με την πράξη, με την εφαρμογή, με την επίλυση του ερωτήματος περί τίνος χρησιμεύουν τα μαθηματικά, όχι απλώς με την εκτέλεση ασκήσεων.

ΟΤΑΝ Η ΜΑΘΗΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΔΕΝ ΕΙΝΑΙ ΠΛΕΟΝ Η ΦΥΣΗ ΤΗΣ ΜΑΘΗΣΗΣ ΜΑΘΗΜΑΤΙΚΩΝ

Σύμφωνα με τον Δρ. Vu Thi Ngoc Ha, από το Ινστιτούτο Εφαρμοσμένων Μαθηματικών και Πληροφορικής του Πανεπιστημίου Επιστήμης και Τεχνολογίας του Ανόι, κάθε μάθημα των φυσικών επιστημών προάγει την ανάπτυξη και την τελειοποίηση της σκέψης σε κάθε παιδί, κάτι που ονομάζεται «ποικιλομορφία των θεμελιωδών πεδίων», όχι απλώς η εκμάθηση μαθηματικών που αναπτύσσει τη σκέψη.

Ωστόσο, στα μαθηματικά, τα προβλήματα σχετίζονται πάντα με την πραγματικότητα. Για να περάσει το παιδί, πρέπει να ακολουθήσει τα βήματα της κατασκευής του προβλήματος με βάση την ανάλυση των νόμων των φυσικών φαινομένων και στη συνέχεια να χρησιμοποιήσει τη λογική σκέψη, τη δημιουργική σκέψη... για να λύσει το πρόβλημα. Κατά τη διαδικασία, μερικές φορές διεγείρεται η φαντασία και η κριτική σκέψη για την επίλυση του προβλήματος.

«Τα ίδια τα μαθηματικά φαίνεται να είναι το μάθημα που διεγείρει την πιο τέλεια σκέψη. Έτσι, η γέννηση των κέντρων «μαθηματικής σκέψης» είναι κατανοητή στην τρέχουσα κατάσταση, όταν πρέπει να αντιμετωπίσουμε το έργο της κατάκτησης μιας συγκεκριμένης ενότητας γνώσης κάθε μαθήματος σε πολύ σύντομο χρονικό διάστημα, όχι μόνο των μαθηματικών, για να αντιμετωπίσουμε τις εξετάσεις. Από εκεί και πέρα, η εκμάθηση μαθηματικών δεν είναι πλέον πιστή στη φύση της «εκμάθησης μαθηματικών», σχολίασε ο Δρ. Ngoc Ha.

Ο καθηγητής Le Anh Vinh είπε ότι στην αρχή ήταν επίσης αλλεργικός στη λέξη «σκεπτόμενα μαθηματικά». Μετά από μεταγενέστερη έρευνα, αποδείχθηκε ότι η διδασκαλία μαθηματικών χωρίς σκέψη εξακολουθεί να είναι αρκετά δημοφιλής. Ο καθηγητής Vinh σχολίασε: «Αν πούμε ότι διδάσκουμε μαθηματικά εδώ, όχι ότι διδάσκουμε μαθηματικά χωρίς σκέψη, ακούγεται πολύ βαρύ. Επομένως, όταν κάποιος ή κάπου παρουσιάζεται ως διδάσκων σκεπτόμενα μαθηματικά, σημαίνει ότι θέλει να πει ότι διδάσκει μαθηματικά με την πραγματική έννοια της λέξης. Επομένως, το «σκεπτόμενα μαθηματικά» προέρχεται από το γεγονός ότι οι άνθρωποι θέλουν να διδάσκουν μαθηματικά έτσι ώστε οι μαθητές να πρέπει να σκέφτονται και να είναι σε θέση να τα εφαρμόζουν στη ζωή, όχι να διδάσκουν μαθηματικά με μια μορφή, έτσι ώστε οι μαθητές να παίρνουν πολύ καλές βαθμολογίες στις εξετάσεις. Οι γονείς θα πρέπει επίσης να λάβουν υπόψη, γιατί όταν παρουσιάζονται έτσι, σημαίνει ότι δεν διδάσκουν στους μαθητές να μαθαίνουν μαθηματικά για να τα πάνε καλά στις εξετάσεις, αλλά διδάσκουν στους μαθητές να σκέφτονται».

ΑΠΑΡΑΙΤΗΤΟ ΓΙΑ ΚΑΙΝΟΤΟΜΙΑ ΣΤΙΣ ΕΞΕΤΑΣΕΙΣ

Ο Δρ. Νγκοκ Χα πιστεύει ότι για να επιστρέψει η μάθηση των μαθηματικών στην πραγματική της φύση, οι μαθητές πρέπει να «μαθαίνουν αργά», επειδή η «αργή μάθηση» είναι ο πιο τέλειος τρόπος για να τονωθεί η ανάπτυξη της σκέψης κάθε παιδιού.

Όταν αντιμετωπίζουν ένα πρόβλημα, οι μαθητές πρέπει να έχουν χρόνο (πολύ μεγάλο χρονικό διάστημα) για να εντοπίσουν φυσικά φαινόμενα, στη συνέχεια να αναζητήσουν ποσότητες και κανόνες για να βρουν τη σχέση μεταξύ των ποσοτήτων μεταξύ τους μέσω εκφράσεων και στη συνέχεια να αναζητήσουν μεθοδολογικά εργαλεία για την επίλυση του προβλήματος. Έτσι, η δημιουργία ενός προγράμματος που ονομάζεται «μαθηματικά σκέψης» είναι πολύ δύσκολη. Αλλά η διδασκαλία είναι ακόμη πιο δύσκολη, επειδή εκτός από το να καθοδηγεί «αργά πολύ αργά», ο δάσκαλος πρέπει να έχει αρκετές γενικές γνώσεις σε υψηλό επίπεδο. Η διδασκαλία πρέπει να είναι ευέλικτη και κατάλληλη για τις ιδιότητες και τις ικανότητες κάθε μαθητή. Αυτό είναι πολύ δύσκολο να γίνει όταν αντιμετωπίζουμε την πίεση της ακαδημαϊκής επίδοσης, που πρέπει να έχουμε βραβεία, βαθμολογίες και προσδοκίες από τους γονείς, σχετικά με τον χρόνο του παιδιού...

Διδάξτε στους μαθητές να σκέφτονται, όχι να υπολογίζουν.

Ο καθηγητής Le Anh Vinh συχνά λέει αστειευόμενος στους καθηγητές μαθηματικών: το να διδάξεις στους μαθητές να σκέφτονται για 10 λεπτά είναι πιο δύσκολο από το να τους μάθεις να κάθονται και να υπολογίζουν για μια ώρα. Αν το να πηγαίνεις σχολείο είναι απλώς να παίρνεις ένα φύλλο εργασίας και να κάθεσαι και να υπολογίζεις όσο το δυνατόν πιο γρήγορα και καλά, τότε στο τέλος του μαθήματος, τίποτα δεν θα μείνει στο μυαλό των μαθητών. Όταν αντιμετωπίζουν νέες καταστάσεις, οι μαθητές δεν μπορούν να σκεφτούν, δεν μπορούν να εφαρμόσουν όσα έχουν μάθει για να λύσουν προβλήματα. Ωστόσο, αυτό είναι ένα συστηματικό πρόβλημα, από την ιστορία των εξετάσεων, των τεστ και των τύπων ασκήσεων, που αναγκάζει τους ανθρώπους να παραλείπουν όλα τα μέρη που αναπτύσσουν τη σκέψη, εστιάζοντας μόνο στο να διδάξουν στους μαθητές να υπολογίζουν και να κάνουν ασκήσεις.

Συγκεκριμένα, για να διδάξουμε τα μαθηματικά ως διδασκαλία της σκέψης απαιτείται ο συγχρονισμός ενός ολόκληρου συστήματος: πρόγραμμα, σχολικά βιβλία, χρόνος κάθε ώρα και κάθε λεπτό, κάθε μάθημα, σύστημα εξετάσεων, κοινωνική ψυχολογία...

Υποψήφιοι της 9ης τάξης στην πόλη Χο Τσι Μινχ στην αίθουσα εξετάσεων μαθηματικών των πρόσφατων εισαγωγικών εξετάσεων της 10ης τάξης. Οι εξετάσεις μαθηματικών είχαν πολλά πρακτικά προβλήματα.

Σύμφωνα με τον καθηγητή Βιν, το νέο πρόγραμμα γενικής εκπαίδευσης επικεντρώνεται στη σύνδεση των μαθηματικών με την πραγματικότητα, με την εφαρμογή τους και στην επίλυση του ερωτήματος γιατί μαθαίνουμε μαθηματικά, όχι απλώς κάνοντας ασκήσεις.

Η Δρ. Phi Le είπε ότι υποστηρίζει τους φοιτητές που παρακολουθούν επιπλέον μαθήματα σε θέματα που τους ενδιαφέρουν και τους είναι ικανοί, αλλά με τρόπο που ενισχύει τη δημιουργικότητα και την ικανότητα σκέψης τους. Η παρακολούθηση επιπλέον μαθημάτων με τη μορφή προετοιμασίας για τις εξετάσεις όπως είναι τώρα δεν είναι πολύ ωφέλιμη για τους φοιτητές. «Το πρόβλημα είναι ότι ο τρόπος με τον οποίο τίθενται οι ερωτήσεις σήμερα κάνει τους φοιτητές που δεν έχουν μελετήσει ποτέ τα είδη ερωτήσεων στις εξετάσεις να γίνονται «ηττημένοι». Το τρέχον εξεταστικό περιβάλλον έχει άνισο ανταγωνισμό μεταξύ των φοιτητών που μαθαίνουν να «σκέφτονται» και των φοιτητών που μαθαίνουν να προετοιμάζονται για τις εξετάσεις. Η σκέψη απαιτεί πολύ χρόνο και αποδοχή του κινδύνου να μην γνωρίζεις πολλά είδη ερωτήσεων. Αυτό είναι το «κίνητρο» που κάνει τους φοιτητές «αναγκασμένους» να παρακολουθούν επιπλέον μαθήματα.

«Πώς, λοιπόν, πρέπει να γίνονται οι εξετάσεις για την ανάπτυξη της σκέψης των μαθητών; Οι ερωτήσεις των εξετάσεων δεν πρέπει να είναι περίπλοκες, πρέπει να συνάδουν με το περιεχόμενο που διδάσκεται στα γενικά σχολεία και πρέπει επίσης να ανακαλύπτουν μαθητές με καλή σκέψη», δήλωσε ο Δρ. Phi Le.

Σύνδεσμος πηγής: https://thanhnien.vn/phai-chang-hoc-sinh-dang-hoc-toan-khong-tu-duy-185230609045433219.htm