Los científicos encuentran solución a un problema clásico de geometría que duró más de un siglo

Ilustración para problema de geometría.

Según el South China Morning Post, el matemático Hong Wang –actualmente profesor asociado del Instituto Courant de Ciencias Matemáticas de la Universidad de Nueva York (EE.UU.)– y su colega Joshua Zahl (Universidad de Columbia Británica, Canadá) acaban de resolver uno de los problemas de geometría más difíciles de los siglos XX y XXI: la conjetura de Kakeya en el espacio tridimensional.

Hong Wang nació en la ciudad de Guilin (China), estudió en la Universidad de Pekín antes de enseñar e investigar en Estados Unidos.

El problema se originó en 1917, cuando el matemático japonés Sōichi Kakeya planteó la pregunta: "¿Cuál es el área mínima necesaria para girar una aguja 180 grados?". Ese espacio mínimo se denomina "conjunto de Kakeya".

En el espacio bidimensional, girar la aguja para formar un círculo es fácil de visualizar, pero si la rotación es más flexible, como agitar la aguja mientras gira, el área que barre la aguja puede ser incluso más pequeña.

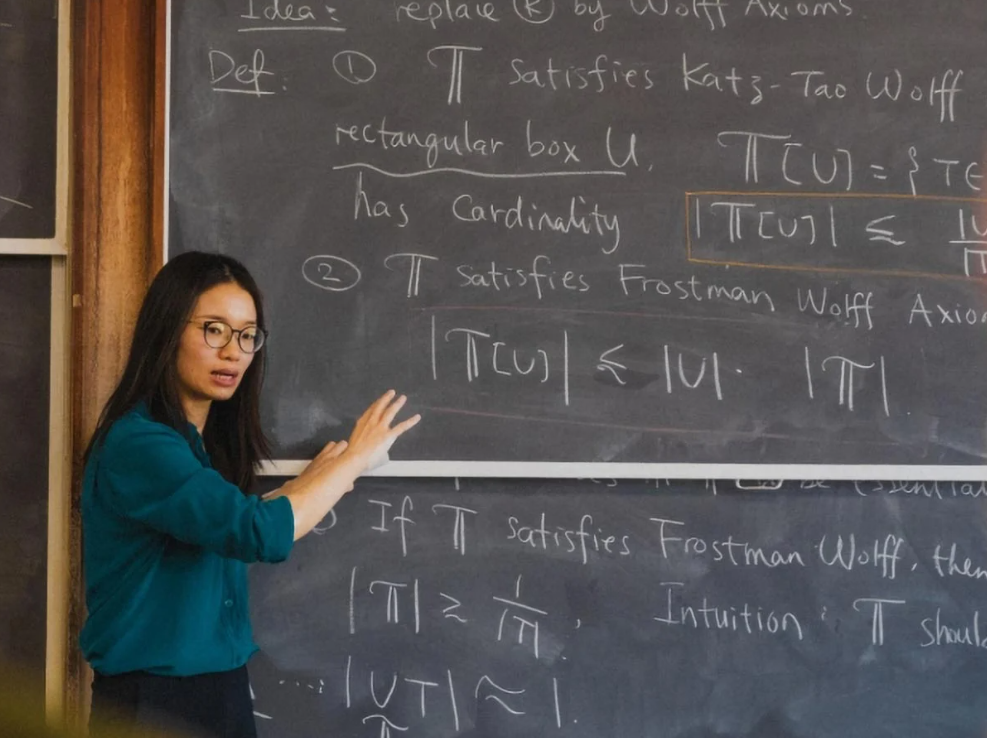
Los científicos encuentran solución a un problema de geometría que duró más de un siglo.

Trasladar el problema a tres dimensiones lo complica mucho más. La conjetura de Kakeya afirma que, para girar la aguja en todas las direcciones, el espacio necesario debe ser lo suficientemente grande en las tres dimensiones; no se puede comprimir en un lugar demasiado pequeño o demasiado estrecho.

En su trabajo, publicado en la plataforma arXiv, Wang y Zahl demuestran que, en el espacio tridimensional, la región donde gira la aguja no necesita tener una forma definida, sino que debe ser lo suficientemente grande en las tres dimensiones. Gracias a ello, resolvieron este problema, considerado un descubrimiento muy importante en las matemáticas actuales.

El profesor Terence Tao, uno de los matemáticos más destacados del mundo , calificó este trabajo de "progreso espectacular". Los expertos también afirmaron que el trabajo no solo amplió la comprensión de la geometría, sino que también podría influir en muchos campos, como el procesamiento de imágenes, las comunicaciones inalámbricas, la informática y la criptografía, donde comprender los movimientos e interacciones en el espacio es fundamental.

"No es una exageración, pero es una solución poco común que hemos estado esperando durante cientos de años", afirmó el profesor de matemáticas Nets Katz, que enseña en la Universidad Rice (EE.UU.).

Según el profesor Guth Larry, profesor del Instituto Tecnológico de Massachusetts (EE. UU.), la hipótesis de Kakeya constituye la base de una "torre" de hipótesis más amplias en el campo de la geometría. Resolver esta hipótesis permitirá alcanzar y superar los niveles superiores de la torre del conocimiento.

"Solía pensar que se trataba de un problema geométrico simple y básico, pero en realidad es demasiado difícil. Este problema ha sido abordado por muchas figuras importantes en el campo de las matemáticas, pero la mayoría solo logró resultados pequeños, no fue sistemático y no pudo considerarse una solución completa", compartió el profesor Guth Larry.

Phuong Anh (Fuente: Science Daily, SCMP)

Fuente: https://vtcnews.vn/gioi-khoa-hoc-tim-ra-loi-giai-bai-toan-hinh-hoc-kinh-dien-keo-dai-hon-mot-the-ky-ar939485.html