आयत के क्षेत्रफल की गणना का सूत्र

एक आयत के क्षेत्र की गणना करने के लिए, लंबाई को चौड़ाई से गुणा करने के अलावा, एक पक्ष को जानने और विकर्ण या परिधि को जोड़ने पर भी गणना करना संभव है।

त्वरित देखें:

• आयत क्या है?
• आयत के क्षेत्रफल की गणना का सूत्र
• 1 भुजा और विकर्ण ज्ञात होने पर आयत का क्षेत्रफल ज्ञात करने का सूत्र
• परिधि ज्ञात होने पर आयत के क्षेत्रफल की गणना करने का सूत्र
• आयत को पहचानने के लिए संकेत?
• क्या एक आयत एक समांतर चतुर्भुज है?
• क्या आयत एक समद्विबाहु समलम्ब है?

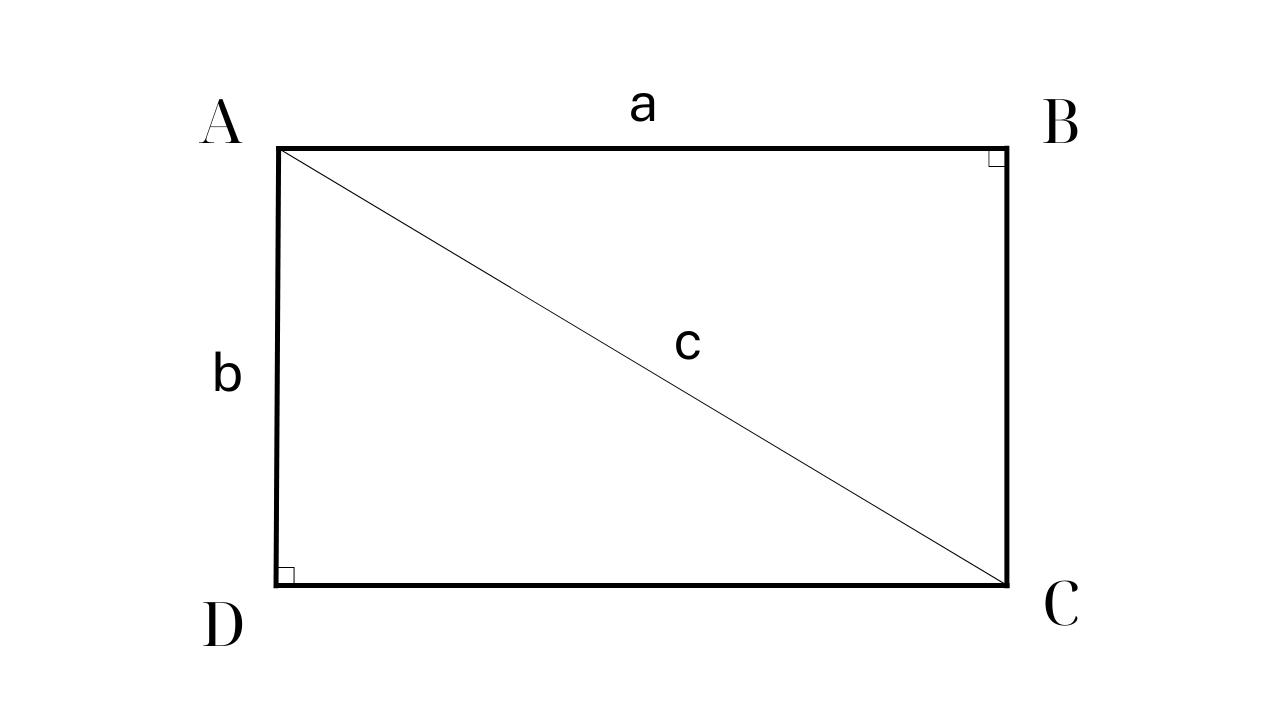
आयत क्या है?

वियतनाम एजुकेशन पब्लिशिंग हाउस की पाठ्यपुस्तक श्रृंखला "ज्ञान को जीवन से जोड़ना" के पाठ 13, गणित 8 (खंड 1) के अनुसार, आयत की परिभाषा 4 समकोण वाला एक चतुर्भुज है।

एक आयत के गुण यह हैं कि इसमें 2 समान्तर विपरीत भुजाएँ, 2 बराबर विपरीत भुजाएँ, 2 बराबर विपरीत कोण, 2 बराबर विकर्ण होते हैं तथा यह प्रत्येक रेखा के मध्य बिंदु पर प्रतिच्छेद करती है।

आयत के क्षेत्रफल की गणना का सूत्र

वियतनाम एजुकेशन पब्लिशिंग हाउस द्वारा पाठ्यपुस्तक श्रृंखला "ज्ञान को जीवन से जोड़ना" की गणित पुस्तक 3 (खंड 2) के पाठ 52 में, एक आयत के क्षेत्रफल की गणना करने का सूत्र लंबाई को चौड़ाई से गुणा करना (माप की समान इकाई) है।

एस = एक्सबी

वहाँ पर:

S: आयत का क्षेत्रफल

a: आयत की लंबाई

b: आयत की चौड़ाई

उदाहरण के लिए: एक आयताकार लकड़ी के बोर्ड की चौड़ाई 5 सेमी और लंबाई 15 सेमी है। उस लकड़ी के बोर्ड का क्षेत्रफल ज्ञात कीजिए।

उत्तर: लकड़ी के बोर्ड का क्षेत्रफल है: S = 5 x 15 = 75 (सेमी ² )

1 भुजा और विकर्ण ज्ञात होने पर आयत का क्षेत्रफल ज्ञात करने का सूत्र

विकर्ण और एक पक्ष को जानते हुए एक आयत के क्षेत्र की गणना करने के लिए, मूल क्षेत्र सूत्र के साथ पाइथागोरस प्रमेय को संयोजित करना आवश्यक है।

चरण 1: शेष भुजा की लंबाई की गणना करने के लिए समकोण त्रिभुज में पाइथागोरस प्रमेय लागू करें।

चरण 2: आयत के क्षेत्रफल की गणना करने के लिए सूत्र लागू करें: S = axb

उदाहरण के लिए: एक आयत ABCD की AD = 60 सेमी, विकर्ण AC = 100 सेमी है। ABCD का क्षेत्रफल ज्ञात कीजिए।

उत्तर:

चरण 1: समकोण त्रिभुज में पाइथागोरस प्रमेय का उपयोग करके आयत ABCD की शेष भुजा ज्ञात कीजिए।

तदनुसार: AC ² =AB ² +AD ² => AB ² = AC ² - AD ² = 10000 - 3600 = 6400 => AB = 80 (सेमी)

चरण 2: क्षेत्रफल ABCD = AB x AD = 60 x 80 = 4800 (सेमी ² )

परिधि ज्ञात होने पर आयत के क्षेत्रफल की गणना करने का सूत्र

परिधि जानने के दौरान एक आयत के क्षेत्र की गणना करने के लिए, आपको परिधि सूत्र और मूल क्षेत्र सूत्र को संयोजित करना होगा।

चरण 1: आयत की परिधि की गणना करने के सूत्र से P = (a+b) x 2 है, जिसमें P परिधि है, a लंबाई है, b आयत की चौड़ाई है, हमारे पास a = (P/2) - b या b = (P/2) - a है

चरण 2: a या b ज्ञात करने के बाद, आयत का क्षेत्रफल ज्ञात करने के लिए सूत्र लागू करें: S = axb

आयत को पहचानने के लिए संकेत?

वियतनाम एजुकेशन पब्लिशिंग हाउस द्वारा गणित 8 (खंड 1) पाठ्यपुस्तक श्रृंखला "ज्ञान को जीवन से जोड़ना" के पाठ 13 के अनुसार, आयत को पहचानने के संकेत हैं:

- एक चतुर्भुज में 3 समकोण होते हैं (परिभाषा के आधार पर)

- समांतर चतुर्भुज में 1 समकोण होता है

- एक समांतर चतुर्भुज में दो बराबर विकर्ण होते हैं।

- एक समद्विबाहु समलम्ब चतुर्भुज में एक समकोण होता है।

क्या एक आयत एक समांतर चतुर्भुज है?

वियतनाम एजुकेशन पब्लिशिंग हाउस द्वारा गणित 8 (खंड 1) पाठ्यपुस्तक श्रृंखला "ज्ञान को जीवन से जोड़ना" के पाठ 13 के अनुसार, एक आयत में समांतर चतुर्भुज के सभी गुण होते हैं। इसलिए, एक आयत एक विशेष समांतर चतुर्भुज है।

क्या आयत एक समद्विबाहु समलम्ब है?

पाठ 13, गणित 8 (खंड 1) वियतनाम एजुकेशन पब्लिशिंग हाउस द्वारा लिखित पाठ्यपुस्तक श्रृंखला "ज्ञान को जीवन से जोड़ना" में, आयत में समद्विबाहु समलम्ब चतुर्भुज के सभी गुण होते हैं। इसलिए, आयत समद्विबाहु समलम्ब चतुर्भुज का एक विशेष रूप है।

(सिंथेटिक)

स्रोत: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html