يُعرّف كتاب الطائرة الورقية، الرياضيات 3، المجلد 1، المستطيل بأنه شكل به 4 زوايا قائمة، و2 ضلعين طويلين متساويين و2 ضلعين قصيرين متساويين.

يحتوي المستطيل على جميع خصائص شبه المنحرف متساوي الساقين ومتوازي الأضلاع مثل:
- أزواج الأضلاع المتقابلة تكون دائمًا متوازية ومتساوية.
- الزوايا متساوية وقياسها 90 درجة.
- المستطيلات لها تماثل من خلال الأقطار ومن خلال النقاط الوسطى للأضلاع.
- الشكل الرباعي الذي فيه ثلاث زوايا قائمة هو مستطيل.
- شبه منحرف متساوي الساقين بزاوية قائمة واحدة هو مستطيل.
- متوازي الأضلاع الذي فيه زاوية قائمة واحدة هو مستطيل.
- الوجه الذي فيه قطرين متساويين هو مستطيل.
وفقًا لكتاب الرياضيات 3، لحساب محيط المستطيل، نأخذ الطول زائد العرض (نفس وحدة القياس) ثم نضرب في 2.
| ص = (أ+ب) × 2 |
هناك
P هو محيط المستطيل.
أ هو طول المستطيل.
ب هو عرض المستطيل.

على سبيل المثال: احسب محيط مستطيل طوله 6 سم وعرضه 4 سم.
الإجابة: محيط المستطيل هو م = (6+4) × 2 = 20 (سم).
مقارنة المستطيلات والمربعات
| معايير | المستطيل | مربع |
|---|---|---|
| حافة | 4 جوانب، 2 زوج من الأضلاع المتقابلة متساوية | 4 جوانب، جميع الجوانب الأربعة متساوية |
| ركن | 4 زوايا قائمة | 4 زوايا قائمة |
| قطري | قطران متساويان، يتقاطعان في نقطة المنتصف ولكنهما غير متعامدين | قطران متساويان، متقاطعان في منتصفهما، وعموديان على بعضهما البعض. |
| صيغة لحساب المحيط | ص = (أ+ب) × 2 | ص = 4أ |
| صيغة لحساب المساحة | س = محور ب | س = أ2 |
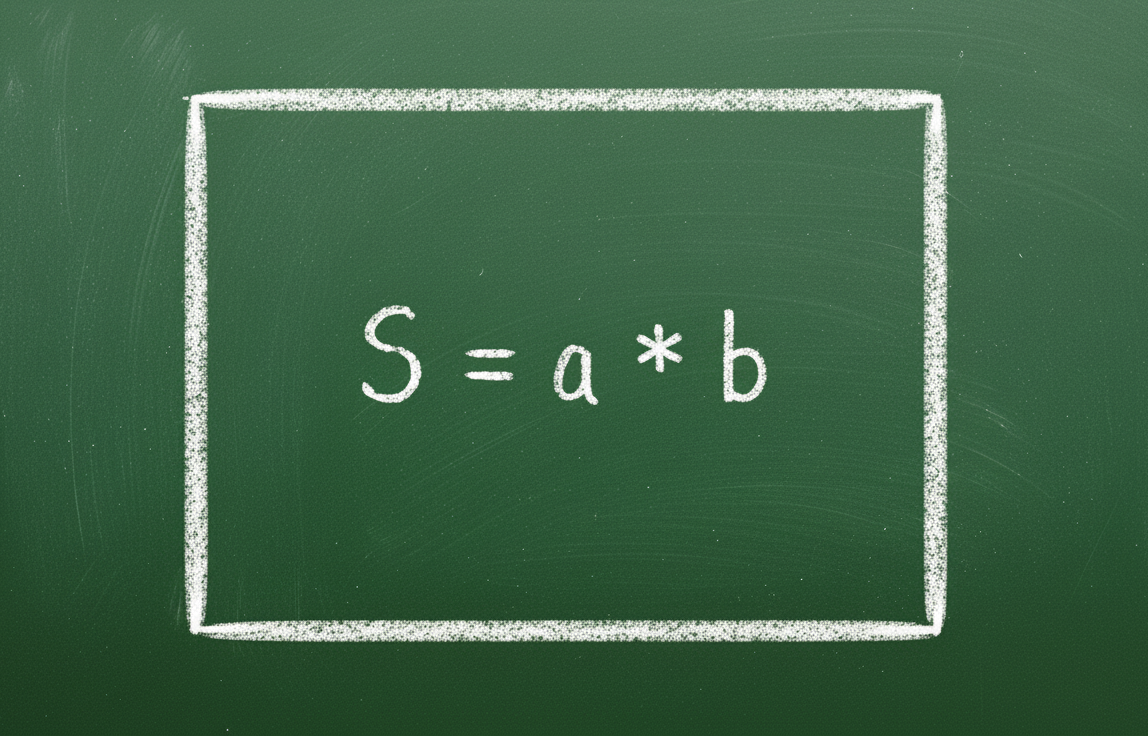
المصدر: https://vietnamnet.vn/cong-thuc-tinh-chu-vi-hinh-chu-nhat-la-gi-2452851.html



![[صورة] انغمس في عالم الموسيقى الملون لـ "Secret Garden Live in Vietnam"](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760805978427_ndo_br_thiet-ke-chua-co-ten-41-png.webp)

![[صورة] جمع النفايات وزرع البذور الخضراء](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760786475497_ndo_br_1-jpg.webp)
![[صورة] حفل اختتام المؤتمر الثامن عشر للجنة الحزب في هانوي](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/17/1760704850107_ndo_br_1-jpg.webp)
![[صورة] الأمين العام تو لام يحضر الذكرى السنوية الخامسة والتسعين لليوم التقليدي للمكتب المركزي للحزب](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760784671836_a1-bnd-4476-1940-jpg.webp)



























































































تعليق (0)