নব্বইয়ের দশকে জন্মগ্রহণকারী মহিলা সহযোগী অধ্যাপক প্রায় একশ বছরের "অত্যন্ত কঠিন" সমস্যা সমাধানে অবদান রেখেছেন

মার্কিন যুক্তরাষ্ট্র - দুই গণিতবিদ, যার মধ্যে একজন তরুণ চীনা ডাক্তারও রয়েছেন, তাদের কাজের মাধ্যমে শতাব্দীর সবচেয়ে জটিল জ্যামিতি সমস্যার সমাধান করা হয়েছে। এই ফলাফলকে "একবিংশ শতাব্দীর গণিতের সবচেয়ে বড় সাফল্য" হিসেবে বিবেচনা করা হয়।

শতাব্দীর সমস্যা

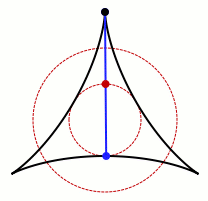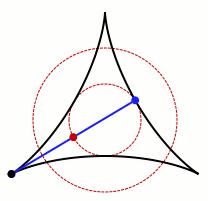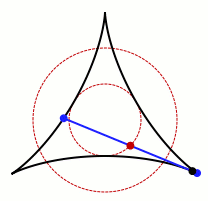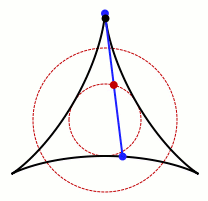
স্মিথসোনিয়ান ম্যাগাজিনের মতে, ১৯১৭ সালে, জাপানি গণিতবিদ সোইচি কাকেয়া সমস্যাটি উত্থাপন করেছিলেন: কীভাবে একটি সূঁচ ৩৬০ ডিগ্রি ঘোরানো যায়, যাতে ঝাঁকুনির ক্ষেত্রটি সবচেয়ে ছোট হয়?

যদি সূঁচটিকে কেন্দ্রের চারপাশে ঘোরানো হয়, তাহলে এটি একটি বৃত্ত তৈরি করবে - তবে গতি সামঞ্জস্য করে ক্ষেত্রফল আরও কমানো যেতে পারে, যেমন ঘোরানোর সময় এটিকে আলতো করে নাড়িয়ে। সেখান থেকে, সমস্যাটি রেখাগুলি কীভাবে ছেদ করতে পারে সেই প্রশ্নে প্রসারিত হয় - একটি আপাতদৃষ্টিতে সহজ প্রশ্ন যার গভীর শিকড় রয়েছে গণিতের অনেক ক্ষেত্রে।

দুই মাত্রায়, কাকেয়ার অনুমান প্রমাণিত হয়েছিল, কিন্তু যখন তিন মাত্রায় স্থানান্তরিত হয়, তখন সমস্যাটি অত্যন্ত জটিল হয়ে ওঠে এবং দশকের পর দশক ধরে অমীমাংসিত থেকে যায়।

মার্কিন যুক্তরাষ্ট্রের নিউইয়র্ক বিশ্ববিদ্যালয়ের ড. ছবি: নিউইয়র্ক ইউনিভার্সিটির ফ্যানপেজ

সম্প্রতি, দুই গণিতবিদ, ভুং হং (নিউ ইয়র্ক বিশ্ববিদ্যালয় - মার্কিন যুক্তরাষ্ট্র) এবং জোশুয়া জাহল (ব্রিটিশ কলাম্বিয়া বিশ্ববিদ্যালয় - কানাডা) ত্রিমাত্রিক স্থানে কাকেয়া অনুমান প্রমাণ করে ১২৭ পৃষ্ঠার একটি গবেষণাপত্র প্রকাশ করেছেন। যদিও এটি আনুষ্ঠানিকভাবে পর্যালোচনা করা হয়নি, তবে গাণিতিক সম্প্রদায় এই গবেষণাপত্রটিকে একটি যুগান্তকারী সাফল্য হিসেবে মূল্যায়ন করেছে।

২০০৬ সালের ফিল্ডস মেডেল বিজয়ী অস্ট্রেলিয়ান-আমেরিকান চীনা বংশোদ্ভূত গণিতবিদ টেরেন্স তাও দ্রুত এই কাজের দিকে নজর দেন। "আমি আনন্দের সাথে ঘোষণা করছি যে জ্যামিতিক পরিমাপ তত্ত্বের সবচেয়ে জনপ্রিয় উন্মুক্ত সমস্যাগুলির মধ্যে একটি, কাকেয়া সেট অনুমান এখন (তিন মাত্রায়) ওয়াং হং এবং জোশুয়া জাহল দ্বারা প্রমাণিত হয়েছে," তাও সামাজিক নেটওয়ার্ক মাস্টোডনে লিখেছেন।

অধ্যাপক ওয়াং হং এবং জাহলের ১২৭ পৃষ্ঠার গবেষণাপত্রটি প্রকাশিত হওয়ার ঠিক একদিন পরেই তার ব্যক্তিগত ব্লগে সারসংক্ষেপ করেছেন, এটিকে জ্যামিতিক পরিমাপ তত্ত্বের ক্ষেত্রে একটি বড় পদক্ষেপ বলে অভিহিত করেছেন।

অধ্যাপক নেটস কাটজ (রাইস বিশ্ববিদ্যালয়, মার্কিন যুক্তরাষ্ট্র) আরও মন্তব্য করেছেন: "এটি একবিংশ শতাব্দীর সর্বশ্রেষ্ঠ গাণিতিক অর্জন হতে পারে। এটি এমন একটি সমস্যার সমাধান করে যা অনেক শীর্ষস্থানীয় গণিতবিদ কাটিয়ে উঠতে পারেননি।"

দুই গণিতবিদ পূর্ববর্তী কাজের উপর ভিত্তি করে স্ক্যানের মাত্রা তিনের কম হওয়ার সম্ভাবনা দূর করার জন্য কাজ করেছিলেন।

সুই ৩৬০ ডিগ্রি ঘোরানোর সমস্যাটি কয়েক দশক ধরে গণিতবিদদের মুগ্ধ করে আসছে।

৯এক্স মহিলা ডাক্তার তরুণ গণিতের এক উজ্জ্বল মুখ

ওয়াং হং চীনের গুইলিনে জন্মগ্রহণ করেন এবং পিকিং বিশ্ববিদ্যালয়ে পড়াশোনা করেন। তিনি বর্তমানে নিউ ইয়র্ক বিশ্ববিদ্যালয়ের (মার্কিন যুক্তরাষ্ট্র) কুরান্ট ইনস্টিটিউট ফর ম্যাথমেটিক্যাল সায়েন্সেসের একজন সহযোগী অধ্যাপক, যেখানে গণিতে তার অসামান্য অবদানের জন্য তাকে সম্মানিত করা হয়েছিল।

চীনা গণমাধ্যমের খবরে বলা হয়েছে, ওয়াং হং ২০০৭ সালে ১৬ বছর বয়সে পিকিং বিশ্ববিদ্যালয়ে পড়াশোনা শুরু করেন এবং ২০১১ সালে গণিতে স্নাতক ডিগ্রি অর্জন করেন।

অনেক অনলাইন মন্তব্যে বলা হয়েছে যে এই সাফল্য তাকে ফিল্ডস মেডেলের প্রার্থী হতে সাহায্য করতে পারে - প্রতি চার বছর অন্তর ৪০ বছরের কম বয়সী গণিতবিদদের জন্য একটি মর্যাদাপূর্ণ গণিত পুরস্কার যা এই ক্ষেত্রে অসামান্য অবদান রেখেছে।

পরবর্তী পুরস্কার প্রদান অনুষ্ঠানটি ২০২৬ সালে আন্তর্জাতিক গণিতবিদদের কংগ্রেসে অনুষ্ঠিত হবে। সম্মানিত হলে, ওয়াং হং হবেন প্রথম চীনা মহিলা যিনি এই মর্যাদাপূর্ণ পদকটি অর্জন করবেন।

এসসিএমপির মতে, ত্রিমাত্রিক স্থানে কাকেয়া অনুমান প্রমাণ করা একটি অগ্রগতি বলে মনে করা হচ্ছে যা ইমেজিং, ডেটা প্রক্রিয়াকরণ, ক্রিপ্টোগ্রাফি এবং ওয়্যারলেস যোগাযোগের মতো ক্ষেত্রগুলিতে বিশাল প্রভাব ফেলতে পারে।

"এটিকে একবিংশ শতাব্দীর শীর্ষ গাণিতিক সাফল্যগুলির মধ্যে একটি হিসাবে বিবেচনা করা হয়," নিউ ইয়র্ক বিশ্ববিদ্যালয়ের কুরান্ট ইনস্টিটিউট ফর ম্যাথমেটিক্যাল সায়েন্সেসের পরিচালক অধ্যাপক ইয়াল লুবেটস্কি বলেছেন।

হাই স্কুল স্নাতক পরীক্ষায় ৩ জন গণিত অধ্যাপক একটিও প্রশ্নের সমাধান করতে পারেননি । অধ্যাপক ডো ডাক থাই একটি বাস্তব ঘটনা শেয়ার করেছেন যে কীভাবে তিনি সহ পেডাগোজিকাল কলেজের ৩ জন গণিত অধ্যাপক ২০২৪ সালের হাই স্কুল স্নাতক পরীক্ষায় একটি প্রশ্নের সমাধান করতে পারেননি।

সূত্র: https://vietnamnet.vn/nu-pho-giao-su-9x-gop-phan-giai-bai-toan-kho-nhat-the-ky-2389893.html