Navrhované matematické odpovědi pro přijímací zkoušky do 10. třídy v Hanoji v roce 2025

Hanojské ministerstvo školství a odborné přípravy oznámilo vzorové otázky pro 7 předmětů pro přijímací zkoušky do 10. ročníku v roce 2025. Mezi těchto 7 předmětů patří literatura, matematika, cizí jazyky, přírodní vědy, dějepis a zeměpis, občanská nauka a informační technologie.

Ilustrativní příklad přijímací zkoušky z matematiky pro 10. ročník ve školním roce 2025 v Hanoji (snímek obrazovky).

V matematice se znalostní zkouška skládá ze 3 částí: Čísla a algebra za 4,5 bodu, geometrie a měření za 4 body a statistika a pravděpodobnost za 1,5 bodu.

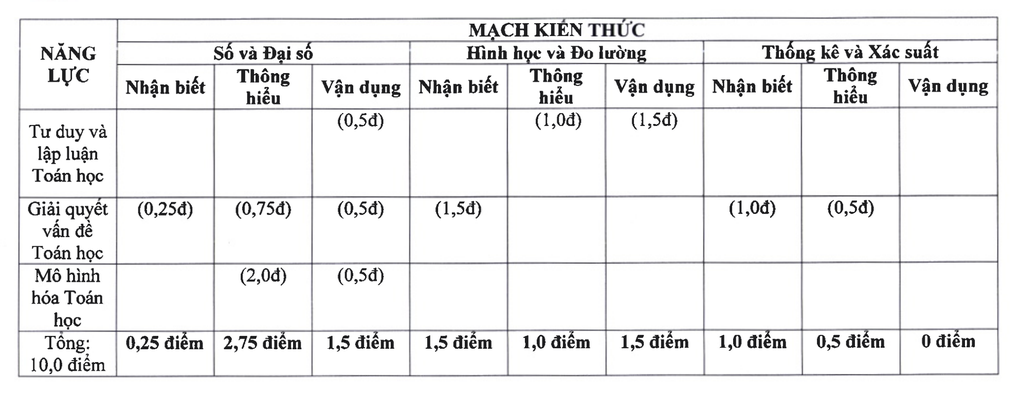
Matematický znalostní okruh pro přijímací zkoušky do 10. ročníku v Hanoji v roce 2025 (snímek obrazovky).

>> Podrobné návrhy odpovědí na zkoušku z matematiky pro 10. ročník v Hanoji v roce 2025 od učitelů odborného oddělení tuyensinh247 naleznete ZDE

Recenze testu s ilustracemi z matematiky

Podle učitele Do Van Bao je obecná struktura zkoušky uspořádána následovně:

Část I: (1,5 bodu) Obsahuje 2 otázky ze statistiky a pravděpodobnosti.

- Statistiky dat, grafy

- Pravděpodobnost

Část II: (1,5 bodu) Zahrnuje 3 otázky týkající se algebraických výrazů, podobné otázce I v předchozích letech.

- Vypočítávejte hodnoty výrazů, otestujte základní dovednosti studentů

- Zjednodušte výraz

- Doplňující otázky k odlišení studentů

Lekce III: (2,5 bodu) Obsahuje 3 otázky týkající se soustav rovnic a kvadratických rovnic.

- Věta 1, 2: Řešte problémy z reálného života sestavením soustavy rovnic, sestavením rovnic

- Otázka 3 Kvadratická rovnice

Lekce IV. Geometrie

- Prostorová geometrie

- Problémy s kruhy

Lekce V. Pokročilé úlohy o geometrických extrémech souvisejících s faktory reálného světa.

Celkové skóre: 10 bodů, rovnoměrně rozdělených mezi základní a pokročilé sekce znalostí, od algebry, geometrie až po praktické aplikace.

Komentáře k znalostnímu obsahu

Algebrická sekce: Zahrnuje základní obsah, jako jsou výpočty s výrazy, kvadratické rovnice a aplikace. Novinkou ukázkového testu je, že obsahuje mnoho otázek, které využívají problémy z reálného života a pomáhají studentům přistupovat k problémům v životě prostřednictvím matematiky.

Geometrická sekce: Zahrnuje známou látku, jako je rovinná geometrie, úlohy týkající se kružnic a vepsaných čtyřúhelníků, prostorová geometrie, geometrické důkazy a geometrické aplikace v praxi. Zkouška vyžaduje, aby studenti měli dobré prostorové myšlení a schopnost aplikovat geometrickou teorii na praktické problémy.

Sekce Statistika a pravděpodobnost: je novým obsahem ve srovnání se zkouškami z předchozího roku, objevuje se v lekci I a vyžaduje od studentů analýzu grafů a výpočet pravděpodobnosti, což je obsahově zaměřeno na praktické využití a často se objevuje v nových učebnicích.

Komentáře k obtížnosti

Základní a středně pokročilá úroveň: Otázky týkající se vyhodnocování výrazů, řešení kvadratických rovnic a výpočtu pravděpodobnosti jsou na základní a středně pokročilé úrovni. Studenti potřebují pouze solidní znalosti základů, aby byli schopni tyto otázky vyřešit.

Pokročilá úroveň: Otázky týkající se geometrických důkazů, praktických problémů zahrnujících prostorovou geometrii a výpočtů bankovních úroků vyžadují od studentů dobré logické myšlení a schopnost aplikovat znalosti v praxi. Tyto otázky budou často náročné pro studenty s průměrnou schopností učení.

Hanojská ukázková zkouška je navržena tak, aby úzce navazovala na nový program všeobecného vzdělávání a zaměřuje se na komplexní prověření znalostí a dovedností studentů, zejména jejich schopnosti aplikovat je v praxi.

Zkouška si zachovává 60–70 % tradiční struktury, ale má inovace v obsahu a metodách kladení otázek, což pomáhá komplexněji hodnotit studenty.

Obtížnost zkoušky je střední, s jasným rozlišováním pro výběr dobrých studentů.

V předchozích letech zkouška často jasně rozlišovala mezi dobrými a průměrnými studenty prostřednictvím čistě algebrových a geometrických otázek. Ukázková zkouška přidala praktické prvky, které od studentů vyžadovaly nejen znalosti, ale také pochopení, jak tyto znalosti aplikovat v konkrétních situacích.

Struktura ilustrativní zkoušky byla letos oproti předchozím letům výrazně inovována, s klasifikací znalostního obsahu v lekcích, prokládáním typů otázek a zejména nárůstem praktických problémů. To odráží orientaci nového vzdělávacího programu, který se více zaměřuje na prověřování schopnosti studentů aplikovat znalosti a syntetizovat myšlení.

Aby žáci 9. ročníku u zkoušky dobře uspěli, potřebují:

Aby se žáci 9. ročníku dobře připravili na přijímací zkoušku do 10. ročníku se stejnou strukturou a obsahem jako vzorová zkouška, musí dodržovat tyto kroky:

1. Pochopte základy

Algebra: Potřeba zvládnout základní znalosti v programu 9. ročníku, včetně:

Rovnice prvního a druhého stupně, řešení a vlastnosti.

Vzorce týkající se rovinné a prostorové geometrie, zejména věty týkající se trojúhelníků, kružnic a základních geometrických tvarů.

Řešení problémů sestavováním rovnic

Geometrie: Znalosti, věty o kružnicích, vepsané čtyřúhelníky a jejich vlastnosti, dokazování podobných trojúhelníků a aplikace vlastností podobných trojúhelníků,...

Statistika a pravděpodobnost: Je nutné se seznámit se základními statistickými pojmy, jako jsou histogramy, frekvenční tabulky a jednoduché výpočty pravděpodobnosti, protože se jedná o části, které se mohou v testu objevit.

2. Procvičte si řešení skutečných matematických problémů

Aplikovaná matematika: Studenti se potřebují seznámit s problémy souvisejícími s reálným životem, s řešením problémů pomocí rovnic, soustav rovnic, s problémy výroby a řízení nebo s problémy souvisejícími s prostorovou geometrií.

Aplikace znalostí v realitě: Procvičování úloh souvisejících s měřením a výpočtem objemu a plochy v praktických situacích. To pomáhá studentům lépe pochopit, jak matematiku aplikovat v životě.

3. Procvičujte si logické myšlení a analytické dovednosti

Matematický důkaz: Procvičování geometrických a algebraických úloh s důkazy. Zejména úlohy vyžadující důkaz vztahů mezi prvky v rovině nebo prostorové geometrii jsou nezbytné pro zlepšení logického myšlení.

Analýza a řešení problémů: Procvičte si analýzu otázek a pochopte požadavky každé otázky, než je začnete řešit. To pomáhá předejít nejasnostem a zvyšuje přesnost procesu skládání testu.

Zdroj: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm