«Πρόβλημα με βραστό νερό» στις εξετάσεις της Α΄ Δημοτικού προκαλεί διαμάχη

Πόλη Χο Τσι Μινχ: Το πρόβλημα του βραστού νερού στις εξετάσεις μαθηματικών της 10ης τάξης προκάλεσε διαμάχη επειδή θεωρήθηκε παράλογο στην πραγματικότητα και λανθασμένο στις γνώσεις φυσικής.

Στις 6 και 7 Ιουνίου, σχεδόν 96.000 υποψήφιοι έδωσαν εξετάσεις Λογοτεχνίας, Ξένων Γλωσσών και Μαθηματικών για να διεκδικήσουν μια θέση στα δημόσια σχολεία της δευτέρας τάξης στην πόλη Χο Τσι Μινχ. Οι εκπαιδευτικοί σχολίασαν ότι η εξέταση των Μαθηματικών είχε την ίδια δομή και δυσκολία με πέρυσι. Η εξέταση περιελάμβανε 5 πρακτικά προβλήματα, από την ερώτηση 3 έως την ερώτηση 7.

Μετά το τέλος των εξετάσεων, ο κ. Mai Van Tuc, καθηγητής Φυσικής στο Λύκειο Φυσικών Επιστημών του Εθνικού Πανεπιστημίου του Ανόι, δήλωσε ότι η ερώτηση 5 στις εξετάσεις Μαθηματικών της 10ης τάξης στην πόλη Χο Τσι Μινχ παρουσίαζε έναν κανόνα που δεν υπάρχει στην πραγματικότητα και είναι λανθασμένος στη φύση του.

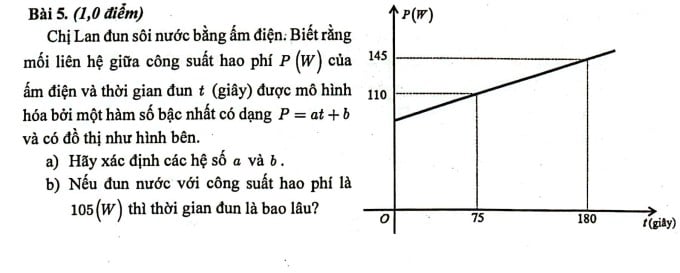
Ερώτηση 5 στις εξετάσεις Μαθηματικών για τις εισαγωγικές εξετάσεις για το δημόσιο σχολείο της 10ης τάξης στην πόλη Χο Τσι Μινχ.

Συγκεκριμένα, η διαδικασία μετατροπής ενέργειας κατά το βράσιμο νερού υπολογίζεται από τη στιγμή που ενεργοποιείται ο διακόπτης (σε t = 0). Η ηλεκτρική ενέργεια μετατρέπεται σε θερμική ενέργεια, καθιστώντας το θερμαντικό καλώδιο ζεστό (εάν ο βραστήρας χρησιμοποιεί θερμαντικό καλώδιο). Το θερμαντικό καλώδιο έχει υψηλότερη θερμοκρασία από το νερό στον βραστήρα και μεταφέρει θερμότητα στο νερό, το νερό μεταφέρει θερμότητα στον βραστήρα και χρειάζεται ένα χρονικό διάστημα για να χαθεί η θερμότητα στο περιβάλλον. Η ικανότητα απώλειας θερμότητας προς το περιβάλλον εξαρτάται κυρίως από την επιφάνεια επαφής του βραστήρα με το περιβάλλον και τη διαφορά θερμοκρασίας μεταξύ της θερμοκρασίας του βραστήρα και του περιβάλλοντος (η ικανότητα απώλειας εξαρτάται επίσης από το επίπεδο κυκλοφορίας του αέρα ή του ανέμου στο σημείο θέρμανσης). Όταν η ικανότητα απώλειας θερμότητας προς το περιβάλλον του βραστήρα είναι ίση με την ισχύ που λαμβάνει το θερμαντικό καλώδιο, η θερμοκρασία του νερού δεν θα αυξάνεται πλέον.

Ο καθηγητής Tuc έδωσε ένα παράδειγμα θερμαντικού καλωδίου χωρητικότητας 1.000 W. Αν βράσει νερό σε έναν βραστήρα 2 λίτρων, το νερό μπορεί να βράσει, αλλά αν αυτό το θερμαντικό καλώδιο παρέχει θερμότητα για ένα μεγάλο ενυδρείο, το νερό μπορεί να θερμανθεί μόνο από 10 βαθμούς Κελσίου έως 30 βαθμούς Κελσίου, τότε η θερμοκρασία δεν θα αυξηθεί άλλο. Εκείνη την ώρα, η απώλεια ισχύος είναι σταθερή και ίση με την κατανάλωση ισχύος του θερμαντικού καλωδίου του βραστήρα. Έτσι, η ερώτηση 5 δίνει την απώλεια ισχύος σύμφωνα με τον κανόνα P = at + b, δηλαδή, t = 0, ο οποίος έχει απώλεια ισχύος 85 W και η απώλεια ισχύος αυξάνεται σταθερά, κάτι που είναι λάθος. Ο καθηγητής πιστεύει επίσης ότι η ερώτηση είναι λάθος όταν ρωτάει "Αν το νερό βράσει με απώλεια ισχύος 105 W, πόσο καιρό θα χρειαστεί για να βράσει;". Αν υποθέσουμε ότι υπάρχει ένας παράλογος κανόνας όπως δίνει ο συγγραφέας, πρέπει να ρωτήσουμε: Υπολογίστε τον χρόνο βρασμού μέχρι η απώλεια ισχύος να είναι 105 W.

Με αυτά τα επιχειρήματα, ο κ. Tuc πρότεινε στο Τμήμα Εκπαίδευσης και Κατάρτισης της πόλης HCM να προσαρμόσει την απάντηση στην ερώτηση 5 για να διασφαλίσει την ισότητα για τους υποψηφίους. Αυτός ο καθηγητής πιστεύει ότι οι μαθητές που είναι καλοί στη Φυσική μπορεί να μην είναι σε θέση να απαντήσουν στην ερώτηση 5 όταν τα δεδομένα στην ερώτηση είναι πολύ περίεργα.

Εν τω μεταξύ, ο κ. Lam Vu Cong Chinh, καθηγητής μαθηματικών στο Λύκειο Nguyen Du στην πόλη Χο Τσι Μινχ, δήλωσε ότι αν λάβουμε υπόψη τη γνώση της Φυσικής και της πραγματικότητας, τα δεδομένα στην ερώτηση 5 δεν είναι λογικά και εύλογα. Ωστόσο, αν η ερώτηση είναι απλώς μια επισκόπηση, σύνθεση και ένας τύπος πρόβλεψης, όχι ένας ακριβής τύπος Φυσικής, εξακολουθεί να είναι αποδεκτή.

Ο κ. Chinh έδωσε ένα παράδειγμα εκτίμησης της αύξησης του πληθυσμού. Σύμφωνα με τον ίδιο, πρόκειται για ένα πρόβλημα που δεν έχει απολύτως ακριβή τύπο, ωστόσο, οι ειδικοί εξακολουθούν να εφαρμόζουν έναν τύπο σύμφωνα με ορισμένους κανόνες και γεγονότα για την πρόβλεψη και την εκτίμηση του μελλοντικού πληθυσμού.

«Εάν οι μαθητές εφαρμόσουν τις μαθηματικές τους γνώσεις, μπορούν να λύσουν το πρόβλημα κανονικά. Αυτό το σφάλμα δεν επηρεάζει τα αποτελέσματα των εξετάσεων των υποψηφίων», δήλωσε ο κ. Chinh.

Η κα Nguyen Tien Thuy, καθηγήτρια μαθηματικών στο Γυμνάσιο Ha Huy Tap στην πόλη Χο Τσι Μινχ, σχολίασε ότι η ερώτηση 5 είναι ένα πρόβλημα συνάρτησης πρώτου βαθμού. Η ερώτηση δίνει τον τύπο για τη συνάρτηση πρώτου βαθμού με σαφείς τύπους για κάθε ποσότητα και μονάδα, μαζί με γραφικές απεικονίσεις, ώστε οι μαθητές να μπορούν να την λύσουν κανονικά.

Οι υποψήφιοι συνομιλούν μετά τις εξετάσεις Μαθηματικών, το πρωί της 7ης Ιουνίου. Φωτογραφία : Le Nguyen

Στις 9 Ιουνίου, το Τμήμα Παιδείας και Κατάρτισης της πόλης Χο Τσι Μινχ ανακοίνωσε ότι η ερώτηση 5 των εισαγωγικών εξετάσεων μαθηματικών της 10ης τάξης έθεσε περιεχόμενο που σχετίζεται με το πραγματικό φαινόμενο της διαδικασίας βρασμού νερού σε ηλεκτρικό βραστήρα. Αυτή η διαδικασία έρευνας είναι μόνο ένα σύντομο στάδιο της διαδικασίας βρασμού νερού και ο χρόνος έναρξης της έρευνας (t = 0) δεν είναι ο χρόνος έναρξης της διαδικασίας βρασμού νερού.

Με τα δεδομένα που ερευνώνται σε αυτή τη διαδικασία, μαθηματικά μπορεί να περιγραφεί ως ένα σχέδιο και από μια συνάρτηση που οι μαθητές έχουν μάθει στο πρόγραμμα. Επομένως, με μαθηματικές γνώσεις και ικανότητες (συνάρτηση πρώτου βαθμού, γραφική παράσταση συνάρτησης πρώτου βαθμού, σημεία σε γραφική παράσταση, σύστημα εξισώσεων πρώτου βαθμού με δύο αγνώστους, υπολογισμός) οι μαθητές μπορούν να λύσουν τις απαιτήσεις που τίθενται από την ερώτηση.

«Σε περιπτώσεις όπου οι μαθητές έχουν λύσεις που διαφέρουν από τις οδηγίες βαθμολόγησης αλλά είναι λογικές, αυτές θα ληφθούν υπόψη και θα αξιολογηθούν», δήλωσε το Υπουργείο Πληροφοριών.

Πέρυσι, περίπου το 45% των υποψηφίων που έδωσαν τις εισαγωγικές εξετάσεις της 10ης τάξης στην πόλη Χο Τσι Μινχ σημείωσαν βαθμολογία κάτω του μέσου όρου στα Μαθηματικά.

Φέτος, στην πόλη Χο Τσι Μινχ περίπου 96.000 μαθητές δίνουν τις δημόσιες εξετάσεις εισαγωγής της 10ης τάξης. Ο συνολικός αριθμός εισακτέων για 108 δημόσια λύκεια στην πόλη είναι 77.300, με ποσοστό εισαγωγής περίπου 80%. Το Υπουργείο Παιδείας και Κατάρτισης δήλωσε ότι οι βαθμολογίες των εξετάσεων θα ανακοινωθούν στις 20 Ιουνίου.

Λε Νγκουγιέν

Σύνδεσμος πηγής: https://vnexpress.net/bai-toan-dun-soi-nuoc-de-thi-lop-10-gay-tranh-cai-4615663.html