Sugerowane odpowiedzi z matematyki na egzamin wstępny do 10. klasy w Hanoi w 2025 r.

Departament Edukacji i Szkolenia w Hanoi ogłosił przykładowe pytania z 7 przedmiotów na egzaminie wstępnym do 10. klasy w 2025 roku. Te 7 przedmiotów obejmuje literaturę, matematykę, języki obce, nauki przyrodnicze, historię i geografię, wiedzę o społeczeństwie oraz technologie informacyjne.

Przykładowy egzamin z matematyki na egzamin wstępny do klasy 10 w roku szkolnym 2025 w Hanoi (zrzut ekranu).

W przypadku matematyki egzamin składa się z 3 części: liczby i algebra – 4,5 punktu, geometria i pomiary – 4 punkty, statystyka i prawdopodobieństwo – 1,5 punktu.

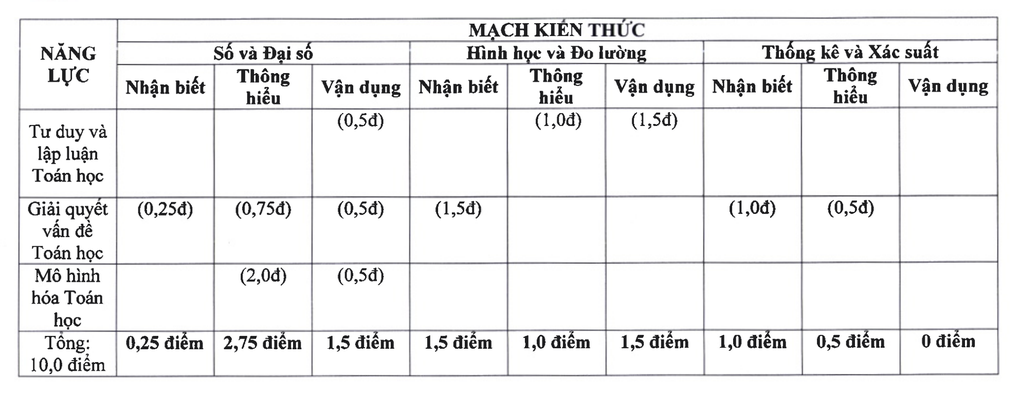
Obwód wiedzy matematycznej na egzaminie wstępnym do 10. klasy w Hanoi w 2025 r. (zrzut ekranu).

>> Zobacz szczegółowe propozycje odpowiedzi na pytania z egzaminu z matematyki dla klasy 10 w Hanoi w 2025 roku od nauczycieli wydziału zawodowego tuyensinh247 TUTAJ

Test powtórkowy z ilustracji matematycznej

Według nauczyciela Do Van Bao ogólna struktura egzaminu wygląda następująco:

Część I: (1,5 punktu) Zawiera 2 pytania z zakresu statystyki i rachunku prawdopodobieństwa.

- Statystyki danych, wykresy

- Prawdopodobieństwo

Część II: (1,5 punktu) Zawiera 3 pytania dotyczące wyrażeń algebraicznych, podobne do pytania I na egzaminach z poprzednich lat.

- Oblicz wartości wyrażeń, sprawdź podstawowe umiejętności uczniów

- Uprość wyrażenie

- Dodatkowe pytania mające na celu różnicowanie uczniów

Lekcja III: (2,5 punktu) Obejmuje 3 pytania dotyczące układów równań i równań kwadratowych.

- Zdania 1,2: Rozwiązuj problemy z życia realnego, tworząc układ równań, tworząc równania

- Pytanie 3 Równanie kwadratowe

Lekcja IV. Geometria

- Geometria przestrzenna

- Problemy z okręgami

Lekcja V. Zaawansowane problemy dotyczące ekstremów geometrycznych w odniesieniu do czynników rzeczywistych.

Łączny wynik: 10 punktów, równomiernie rozłożonych pomiędzy sekcje wiedzy podstawowej i zaawansowanej, od algebry, przez geometrię, po zastosowania praktyczne.

Komentarze dotyczące treści wiedzy

Sekcja Algebra: Obejmuje podstawowe treści, takie jak obliczenia z wyrażeniami, równania kwadratowe i zastosowania. Nowością w tym przykładowym teście jest to, że zawiera wiele pytań wykorzystujących rzeczywiste problemy, pomagając uczniom w rozwiązywaniu problemów w życiu codziennym poprzez matematykę.

Sekcja Geometria: Obejmuje znane treści, takie jak geometria płaska, zagadnienia związane z okręgami i czworokątami wpisanymi, geometria przestrzenna, dowody geometryczne oraz praktyczne zastosowania geometrii. Egzamin wymaga od studentów dobrego myślenia przestrzennego i umiejętności stosowania teorii geometrycznej do problemów praktycznych.

Sekcja Statystyka i prawdopodobieństwo: to nowa treść w porównaniu z egzaminami z poprzednich lat, pojawiająca się w lekcji I, wymagająca od uczniów analizowania wykresów i obliczania prawdopodobieństwa, co ma zastosowanie praktyczne i często pojawia się w nowych programach podręcznikowych.

Komentarze dotyczące trudności

Poziom podstawowy i średnio zaawansowany: Pytania dotyczące obliczania wyrażeń, rozwiązywania równań kwadratowych i obliczania prawdopodobieństwa są na poziomie podstawowym i średnio zaawansowanym. Aby móc odpowiedzieć na te pytania, uczniowie muszą jedynie dobrze opanować podstawy.

Poziom zaawansowany: Pytania dotyczące dowodów geometrycznych, praktycznych problemów z geometrii przestrzennej oraz obliczania odsetek bankowych wymagają od uczniów dobrego logicznego myślenia i umiejętności stosowania wiedzy w praktyce. Pytania te często będą stanowić wyzwanie dla uczniów o przeciętnych zdolnościach uczenia się.

Przykładowy egzamin w Hanoi został opracowany tak, aby ściśle odpowiadał nowemu programowi kształcenia ogólnego, i kładzie nacisk na kompleksowe sprawdzanie wiedzy i umiejętności uczniów, zwłaszcza ich zdolności do zastosowania ich w praktyce.

Egzamin zachowuje 60–70% tradycyjnej struktury, ale wprowadza innowacje w zakresie treści i metod formułowania pytań, co pozwala na bardziej wszechstronną ocenę uczniów.

Stopień trudności egzaminu jest umiarkowany, z wyraźnym zróżnicowaniem mającym na celu wyłonienie dobrych uczniów.

W poprzednich latach egzamin często wyraźnie rozróżniał uczniów dobrych i przeciętnych, wykorzystując pytania z algebry i geometrii. Przykładowy egzamin zawierał elementy praktyczne, wymagające od uczniów nie tylko posiadania wiedzy, ale także umiejętności jej zastosowania w konkretnych sytuacjach.

Struktura egzaminu ilustracyjnego w tym roku została znacząco udoskonalona w porównaniu z poprzednimi latami, z podziałem na treści nauczania, przeplataniem różnych typów pytań, a zwłaszcza zwiększeniem liczby zadań praktycznych. Odzwierciedla to orientację nowego programu nauczania, który koncentruje się na sprawdzaniu umiejętności uczniów w zakresie stosowania wiedzy i syntezy myślenia.

Aby dobrze zdać egzamin, uczniowie klasy 9. muszą:

Aby dobrze przygotować się do egzaminu wstępnego do klasy 10, o takiej samej strukturze i treści jak egzamin przykładowy, uczniowie klasy 9 powinni wykonać następujące kroki:

1. Zrozum podstawy

Algebra: Konieczne jest opanowanie podstawowej wiedzy z programu 9. klasy, w tym:

Równania pierwszego i drugiego stopnia, rozwiązania i właściwości.

Wzory dotyczące geometrii płaskiej i bryłowej, szczególnie twierdzenia dotyczące trójkątów, okręgów i podstawowych figur geometrycznych.

Rozwiązuj problemy, układając równania

Geometria: Wiedza, twierdzenia o okręgach, czworokątach wpisanych i własnościach, dowodzenie podobieństwa trójkątów i stosowanie własności trójkątów podobnych,...

Statystyka i rachunek prawdopodobieństwa: Konieczna jest znajomość podstawowych pojęć statystycznych, takich jak histogramy, tabele częstości, proste obliczenia prawdopodobieństwa, ponieważ mogą się one pojawić na egzaminie.

2. Ćwicz rozwiązywanie prawdziwych problemów matematycznych

Matematyka stosowana: Uczniowie muszą ćwiczyć na problemach związanych z życiem realnym, rozwiązywaniem problemów poprzez układanie równań i układów równań, problemami związanymi z produkcją i zarządzaniem, a także problemami związanymi z geometrią przestrzenną.

Zastosowanie wiedzy w praktyce: Ćwiczenia z mierzenia i obliczania objętości i powierzchni w sytuacjach praktycznych. Pomaga to uczniom lepiej zrozumieć, jak stosować matematykę w życiu.

3. Ćwicz logiczne myślenie i umiejętności analityczne

Dowód matematyczny: Pogłębianie umiejętności rozwiązywania problemów z dowodami geometrycznymi i algebraicznymi. W szczególności problemy wymagające udowodnienia relacji między elementami płaszczyzny lub geometrii przestrzennej są niezbędne do doskonalenia logicznego myślenia.

Analizuj i rozwiązuj problemy: Przećwicz analizę pytań i zrozum wymagania każdego z nich, zanim zaczniesz je rozwiązywać. Pomaga to uniknąć nieporozumień i zwiększa dokładność w procesie zdawania testu.

Source: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm