Kite Book, Mathematik 3, Band 1 definiert ein Rechteck als eine Form mit 4 rechten Winkeln, 2 gleich langen Seiten und 2 gleich kurzen Seiten.

Ein Rechteck hat alle Eigenschaften eines gleichschenkligen Trapezes und eines Parallelogramms, wie zum Beispiel:
- Paare gegenüberliegender Seiten sind immer parallel und gleich.
- Die Winkel sind gleich und betragen 90 Grad.
- Rechtecke sind durch die Diagonalen und durch die Mittelpunkte der Seiten symmetrisch.
- Ein Viereck mit drei rechten Winkeln ist ein Rechteck.
- Ein gleichschenkliges Trapez mit einem rechten Winkel ist ein Rechteck.
- Ein Parallelogramm mit einem rechten Winkel ist ein Rechteck.
- Eine Fläche mit zwei gleich großen Diagonalen ist ein Rechteck.
Um den Umfang eines Rechtecks zu berechnen, nehmen wir laut dem Mathe-3-Lehrbuch die Länge plus die Breite (dieselbe Maßeinheit) und multiplizieren das Ergebnis dann mit 2.
| P = (a+b) x 2 |
Dort drin
P ist der Umfang des Rechtecks.
a ist die Länge des Rechtecks.
b ist die Breite des Rechtecks.

Beispiel: Berechnen Sie den Umfang eines Rechtecks mit einer Länge von 6 cm und einer Breite von 4 cm.
Antwort: Der Umfang des Rechtecks beträgt P = (6+4) x 2 = 20 (cm).
Vergleichen Sie Rechtecke und Quadrate
| Kriterien | Rechteck | Quadrat |
|---|---|---|
| Rand | 4 Seiten, 2 Paare gegenüberliegender Seiten sind gleich | 4 Seiten, alle 4 Seiten sind gleich |
| Ecke | 4 rechte Winkel | 4 rechte Winkel |
| Diagonale | Zwei Diagonalen sind gleich, schneiden sich in der Mitte, sind aber nicht senkrecht | Zwei Diagonalen sind gleich, schneiden sich im Mittelpunkt und stehen senkrecht zueinander. |
| Formel zur Berechnung des Umfangs | P = (a+b) x 2 | P = 4a |
| Formel zur Flächenberechnung | S = axb | S = a2 |
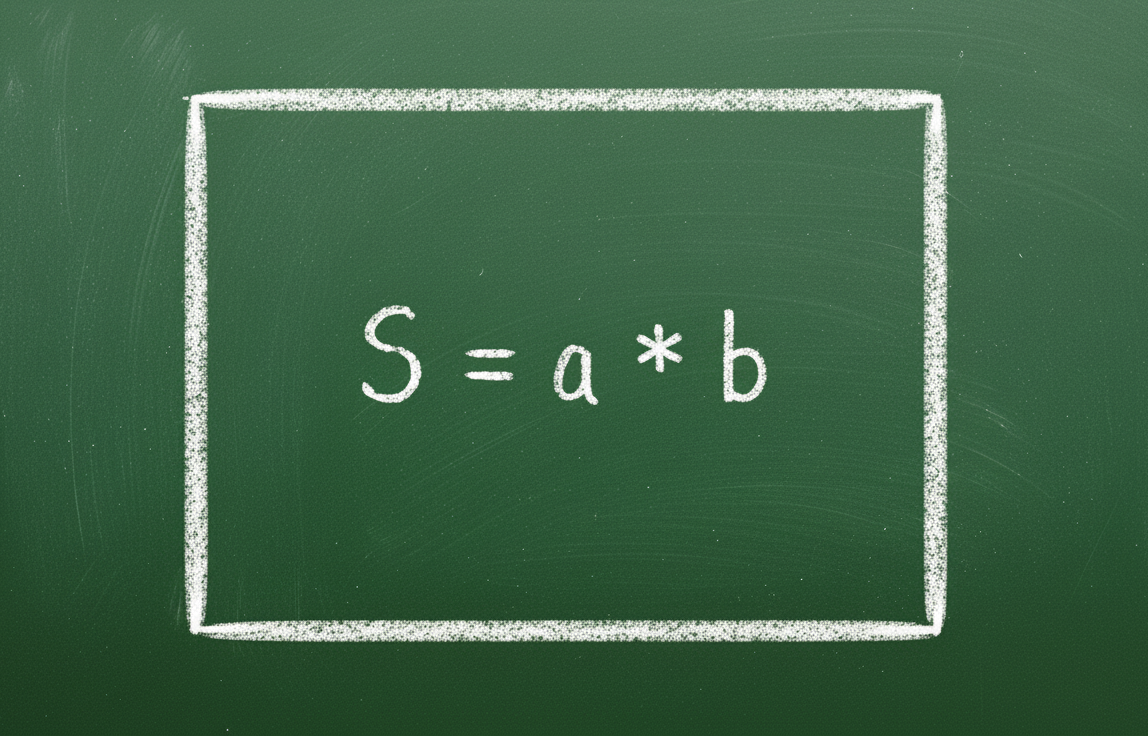
Quelle: https://vietnamnet.vn/cong-thuc-tinh-chu-vi-hinh-chu-nhat-la-gi-2452851.html




![[Foto] Tauchen Sie ein in die farbenfrohe Musikwelt von „Secret Garden Live in Vietnam“](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760805978427_ndo_br_thiet-ke-chua-co-ten-41-png.webp)
![[Foto] Abschlusszeremonie des 18. Kongresses des Parteikomitees von Hanoi](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/17/1760704850107_ndo_br_1-jpg.webp)
![[Foto] Abfall sammeln, grüne Samen säen](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760786475497_ndo_br_1-jpg.webp)
![[Foto] Generalsekretär To Lam nimmt am 95. Jahrestag des Traditionstags der Parteizentrale teil](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760784671836_a1-bnd-4476-1940-jpg.webp)



























































































Kommentar (0)