Drawing a triangle that overflows the edge of the paper, 2 students unexpectedly prove a 2,500-year-old mathematical theorem

What is special is that no one has ever proven the theorem in this way, not even Albert Einstein.

In high school, all of us have had to solve geometry problems. And once we have solved geometry problems, we have all encountered this situation at least once: While drawing a figure, we run out of paper.

All such cases involve a "mutant" triangle, with two unusually long sides, so that no matter how far you draw them, they still don't intersect. How would you handle this situation?

Illustration photo.

Some students—very creatively—will continue drawing the shape in another dimension, which is the back of the paper. Others will take another sheet of paper and place it underneath the first one to complete the shape. Or, if you’re in a pinch, you can draw the triangle floating on the table.

However, some people will think: Why do you insist on drawing that "mutant" triangle? Just draw until the paper runs out, then stop. Even if you can't draw the whole shape on the paper, your solution is definitely not correct.

But a new study in the journal American Mathematical Monthly will now make them think again. Sometimes, the triangles on the outside of a piece of paper can hide unexpected mathematical secrets.

Specifically in this case, with a "mutant" triangle, two high school students in the US found a way to prove the Pythagorean theorem, which was once considered "impossible" for more than 2,500 years, since it was stated.

Illustration photo.

No one has ever proven the Pythagorean theorem this way, not even Albert Einstein.

The Pythagorean theorem is named after the ancient Greek mathematician Pythagoras (570–495 BC), who first proved it, although there is evidence that mathematicians in other ancient civilizations such as Babylon, India, Mesopotamia, and China also independently discovered it:

That in a right triangle, the square of the hypotenuse is always equal to the sum of the squares of the lengths of the other two sides. If a right triangle has sides of length a and b and hypotenuse c, then the Pythagorean Theorem is expressed by the formula:

𝑐 ² = 𝑎 ² + 𝑏 ²

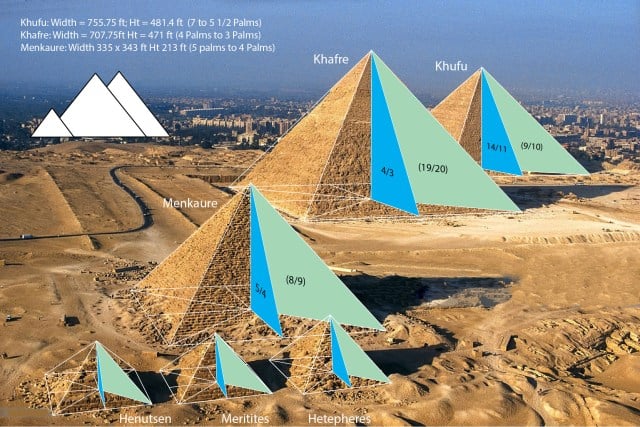
If it weren't for the Pythagorean Theorem, the ancient Egyptians wouldn't have been able to build the pyramids.

It seems like a simple formula, but without knowing the Pythagorean Theorem, the ancient Egyptians would not have been able to build the pyramids, the Babylonians would not have been able to calculate the position of the stars, and the Chinese would not have been able to divide the land.

This theorem also laid the foundation for many schools of mathematics such as solid geometry, non-Euclidean geometry and differential geometry - without which, or if it were proven wrong, almost the entire branch of geometry of mathematics known to mankind today would collapse.

Proving the Pythagorean Theorem was therefore a very important task. As early as 500 BC, the ancient Greek mathematician Pythagoras took on this task and made his name in history for the first time.

He proved the Pythagorean Theorem using a very simple method:

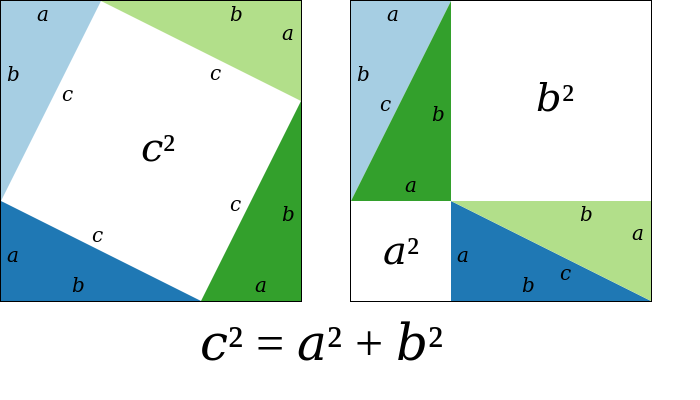
Illustration photo.

Draw a square with side lengths a+b. Then, at each corner, continue to draw 4 equal triangles, with sides a and b. These triangles are all equal right triangles, with hypotenuse c, and together create a space inside the square with area c ² .

Then, just by rearranging the positions of those four triangles, Pythagoras created two new spaces, which are two squares with sides a and b. The total area of ​​those two spaces is a ² + b ² , which of course must be equal to the original space c ² .

This is the proof you'll find in your 7th grade middle school math textbook. But there's another proof of the Pythagorean Theorem that you may not have learned. It's the one Albert Einstein came up with when he was just 11 years old.

Einstein then realized that if he dropped an altitude AD perpendicular to the hypotenuse BC of the right triangle ABC, he would get 2 right triangles similar to the right triangle ABC. Now, just by drawing outside the right triangle ABC squares with sides equal to each of its sides, Einstein would get 3 squares with areas equal to a ² , b ² and c ² .

Since the ratio of the area of ​​a right triangle to the area of ​​a square on its hypotenuse is the same for similar triangles, we will also have 𝑐 ² = 𝑎 ² + 𝑏 ² .

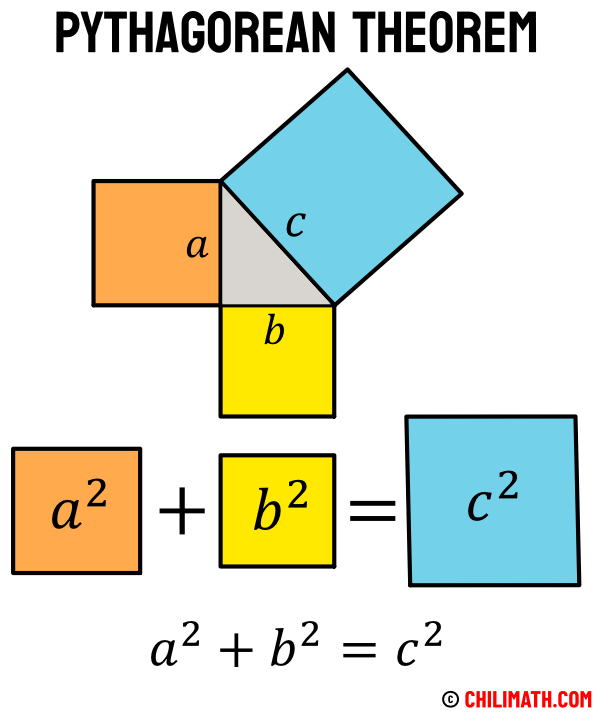
Illustration photo.

However, these are just two of the 370 proofs of the Pythagorean Theorem that mathematicians have found over the past 2,500 years. From using algebra, calculus to various geometrical cuts, this mathematical theorem can be proven true using methods ranging from easy to complex.

However, in all these solutions, there is no proof using trigonometric formulas. Since Pythagoras itself is a fundamental theorem in trigonometry, proving it using trigonometry would lead us into a trap of logical fallacy, called circular thinking, when we use the Pythagorean Theorem itself to prove the Pythagorean Theorem.

Mathematicians have repeatedly failed in this task, so much so that in 1927, American mathematician Elisha Loomis exclaimed: " There is no way to prove the Pythagorean Theorem by trigonometry because all basic trigonometric formulas must rely on the correctness of the Pythagorean Theorem."

But as it turns out, Elisha Loomis was wrong.

Nearly 100 years later, these two high school students have found a way to prove the Pythagorean Theorem using trigonometry.

In a new study published in the journal American Mathematical Monthly, two students, Ne'Kiya Jackson and Calcea Johnson from St. Mary's Academy High School in Colorado, presented not one but 10 ways to prove the Pythagorean Theorem using trigonometry.

Ne'Kiya Jackson (left) and Calcea Johnson (right).

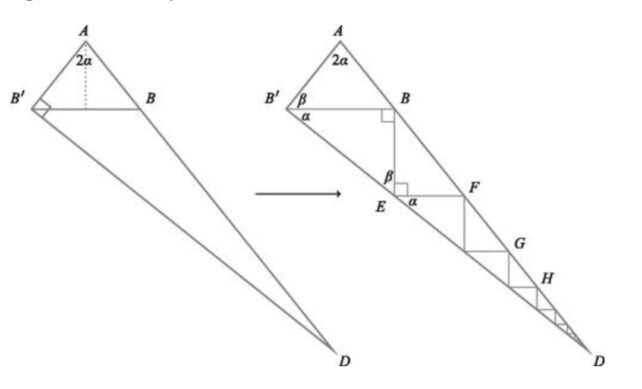
To be able to do this, Jackson and Johnson used a right triangle ABC as usual. " Our first proof begins by flipping triangle ABC over its side AC to form an isosceles triangle ABB' ," the duo wrote in the paper.

In the next step, they will construct a right triangle AB'D, by extending side AB to point D so that from D they can drop a perpendicular to B'A.

At this point, make sure you have enough paper, because AB'D is a triangle with an unusually long side and point D will most likely jump out beyond the edge of your paper.

Then, from point B, you will drop a perpendicular to BB', cutting B'D at E. Then from E, drop a perpendicular to cut AD at F... And so on to infinity, you will get countless similar triangles whose combined areas are equal to the area of ​​triangle AB'D:

Now the important point:

Jackson and Johnson found that since BB' has length 2a and triangle B'EB is similar to triangle ABC, they could calculate the length of side BE as 2a ² /b. BF=2A ² c/b ² . Thus, the sides FG, GH can be calculated as 2a ⁴ c/b ⁴ and 2a ⁶ c/b ⁶ …

Then, the length of the hypotenuse AD will be equal to the sum of the line segments:

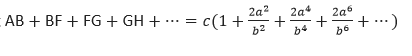
In triangle AB'D, we have:

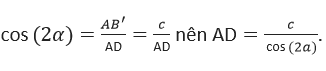
From the two formulas above, we can establish the equation:

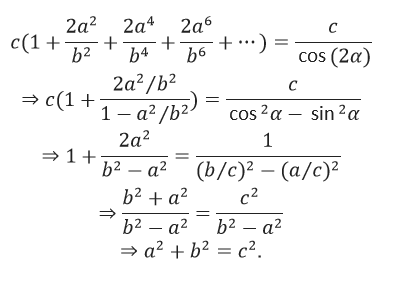
In which, using the sum of a basic convergent series is:

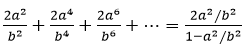
Immediately after its publication, Jackson and Johnson's proof of the Pythagorean Theorem attracted mathematicians, including Álvaro Lozano-Robledo, from the University of Connecticut.

“ It looked like nothing I had ever seen before,” Lozano-Robledo said. The idea of ​​filling a large triangle with infinitely many smaller triangles and then calculating the length of its sides using a convergent series was an unexpected innovation for a high school student.

Mathematician Álvaro Lozano-Robledo of the University of Connecticut praised Ne'Kiya Jackson and Calcea Johnson.

“ Some people think that someone has to spend years in school or research institutes to solve a new problem ,” said Lozano-Robledo. “ But this proves that it can be done while you are still in high school.”

Not only did Jackson and Johnson prove the Pythagorean Theorem in a completely new way, their solution also underscored a delicate boundary of the concept of trigonometry, they said.

" High school students may not realize that there are two versions of trigonometry attached to the same term. In that case, trying to understand trigonometry is like trying to understand a picture with two different images printed on top of each other ," they say.

The surprising solution to the Pythagorean Theorem came from Jackson and Johnson separating these two trigonometric variations and using another fundamental law of trigonometry, the Law of Sines. In this way, the duo avoided the vicious circles that previous mathematicians, including Elisha Loomis, had encountered when they tried to prove the Pythagorean Theorem using the Pythagorean Theorem.

No one has ever proven the Pythagorean theorem this way, not even Albert Einstein.

"Their results have drawn the attention of other students to a new and promising perspective ," said Della Dumbaugh, editor-in-chief of American Mathematical Monthly. comment.

“ It will also open up a lot of new mathematical conversations ,” Lozano-Robledo said. “ That’s when other mathematicians can use this paper to generalize that proof, generalize their ideas, or simply use that idea in other ways.”

It can be seen that a new land in mathematics was opened after Jackson and Johnson drew the mutant " triangle ". A triangle extending beyond the edge of the paper contains inside a loop of endless triangles.

So the next time you’re solving a geometry problem and you come across an edge, try drawing it all the way to the edge. Who knows, you might just make a discovery.

Source: Sciencealert, Sciencenews, Tandfonline

Source: https://phunuvietnam.vn/ve-tam-giac-tran-ra-mep-giay-2-hoc-sinh-bat-ngo-chung-minh-duoc-dinh-ly-toan-hoc-co-tuoi-doi-2500-nam-20241030065904234.htm