El problema de encontrar al gato detrás de la puerta

El problema de matemáticas de quinto grado le pide al lector que calcule el número de puertas que debe abrir para encontrar al gato, sabiendo que después de cada puerta vacía que se abra, el gato se moverá a otra puerta.

Tema:

Un pasillo recto tiene cinco puertas a un lado. Detrás de una de ellas hay un gato. Tu misión es encontrarlo abriendo la puerta correcta. Solo puedes abrir una puerta al día. Si el gato está ahí, ¡ganas!

Si el gato no está, la puerta se cerrará y tendrás que esperar hasta el día siguiente para volver a abrirla. El gato se mueve constantemente y cada noche se coloca detrás de una puerta diferente. La puerta a la que se dirige será la que esté a la izquierda o a la derecha de donde se encuentra actualmente.

¿Cuántos días necesitas para estar seguro de encontrar al gato?

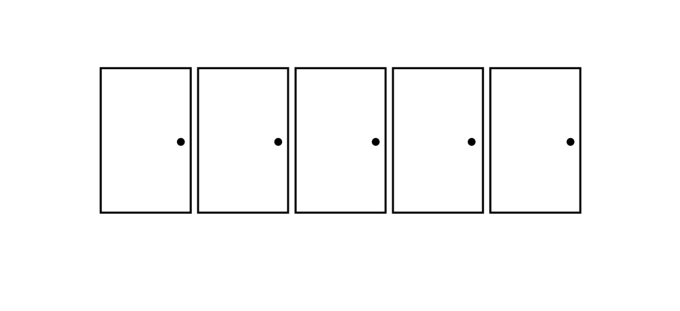
El problema consiste en encontrar una estrategia que garantice atrapar al gato en un número determinado de días, independientemente de la puerta por la que empiece y adónde vaya por la noche. La clave para resolverlo es empezar con pocas puertas, identificar el patrón y luego aumentar el número de puertas.

Supongamos que solo hay tres puertas. Si abres la puerta del medio dos días seguidos, seguro que atraparás al gato, porque si no está detrás de la puerta del medio el primer día, estará detrás de una de las dos puertas de los extremos. Y si está detrás de una de las puertas de los extremos el primer día, no le quedará más remedio que ir a la puerta del medio el segundo día.

Si hay cuatro puertas, puedes atrapar al gato en cuatro días. Encontrarás la explicación en la respuesta de abajo, pero antes, intenta deducirlo tú mismo. Recuerda que el gato solo se mueve a la puerta que está inmediatamente a su derecha o izquierda y puede regresar a la puerta por la que estaba antes. Seguro que te alegrarás cuando encuentres la explicación.

>>>Respuesta

Vo Quoc Ba Can

Profesor de matemáticas, Escuela Arquímedes de Hanói

Enlace de origen: https://vnexpress.net/bai-toan-tim-con-meo-sau-canh-cua-4604654.html