فرمول محاسبه مساحت مستطیل

مستطیل چیست؟

طبق درس ۱۳، ریاضی ۸ (جلد ۱) از مجموعه کتاب‌های درسی «پیوند دانش با زندگی» از انتشارات آموزش ویتنام، تعریف مستطیل، چهارضلعی با ۴ زاویه قائمه است.

ویژگی‌های مستطیل این است که دو ضلع روبروی موازی، دو ضلع روبروی مساوی، دو زاویه روبروی مساوی و دو قطر مساوی دارد و هر خط در نقطه وسط یکدیگر را قطع می‌کنند.

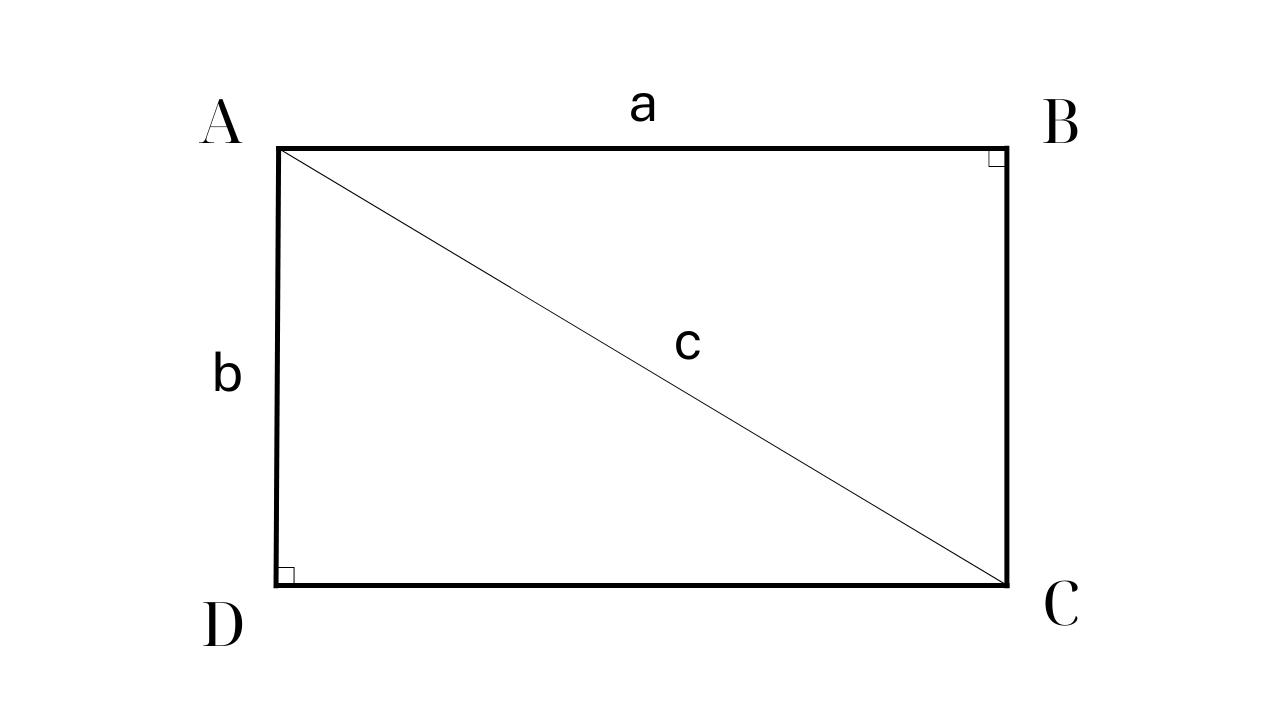
فرمول محاسبه مساحت مستطیل

در درس ۵۲، کتاب ریاضی ۳ (جلد ۲) از مجموعه کتاب‌های درسی «پیوند دانش با زندگی» از انتشارات آموزش ویتنام، فرمول محاسبه مساحت مستطیل، طول ضربدر عرض (همان واحد اندازه‌گیری) است.

S = axb

در آنجا:

S: مساحت مستطیل

الف: طول مستطیل

ب: عرض مستطیل

برای مثال: یک تخته چوبی مستطیل شکل، عرض ۵ سانتی‌متر و طول ۱۵ سانتی‌متر دارد. مساحت آن تخته چوبی را محاسبه کنید.

پاسخ: مساحت تخته چوبی: S = 5 x 15 = 75 (سانتی متر ^مربع )

فرمول محاسبه مساحت مستطیل هنگام دانستن 1 ضلع و مورب

برای محاسبه مساحت مستطیل هنگام دانستن قطر و یک ضلع، لازم است قضیه فیثاغورث را با فرمول اساسی مساحت ترکیب کنید.

مرحله ۱: قضیه فیثاغورث را در یک مثلث قائم‌الزاویه اعمال کنید تا طول ضلع باقیمانده محاسبه شود.

مرحله 2: فرمول را برای محاسبه مساحت مستطیل اعمال کنید: S = axb

برای مثال: مستطیل ABCD دارای AD = 60 سانتی‌متر و قطر AC برابر با 100 سانتی‌متر است. مساحت ABCD را محاسبه کنید.

پاسخ:

مرحله 1: ضلع باقیمانده مستطیل ABCD را با استفاده از قضیه فیثاغورث در یک مثلث قائم الزاویه پیدا کنید.

بر این اساس: AC ² =AB ² +AD ² => AB ² = AC ² - AD ² = 10000 - 3600 = 6400 => AB = 80 (سانتی متر)

مرحله ۲: مساحت ABCD = AB x AD = 60 x 80 = 4800 (سانتی متر ^مربع )

فرمول محاسبه مساحت مستطیل هنگام دانستن محیط

برای محاسبه مساحت مستطیل هنگام دانستن محیط، باید فرمول محیط و فرمول پایه مساحت را با هم ترکیب کنید.

مرحله ۱: از فرمول محاسبه محیط مستطیل، P = (a+b) x 2 است که در آن P محیط، a طول و b عرض مستطیل است. داریم: a = (P/2) - b یا b = (P/2) - a

مرحله 2: پس از پیدا کردن a یا b، فرمول را برای محاسبه مساحت مستطیل اعمال کنید: S = axb

علائم تشخیص مستطیل؟

طبق درس ۱۳، ریاضی ۸ (جلد ۱) از مجموعه کتاب‌های درسی «پیوند دانش با زندگی» اثر انتشارات آموزش ویتنام، نشانه‌های تشخیص مستطیل عبارتند از:

- یک چهارضلعی دارای ۳ زاویه قائمه است (بر اساس تعریف)

- متوازی الاضلاع ۱ زاویه قائمه دارد

- متوازی الاضلاع دو قطر مساوی دارد.

- ذوزنقه متساوی الساقین یک زاویه قائمه دارد.

آیا مستطیل یک متوازی الاضلاع است؟

طبق درس ۱۳، ریاضی ۸ (جلد ۱) از مجموعه کتاب‌های درسی «پیوند دانش با زندگی» اثر انتشارات آموزش ویتنام، مستطیل تمام ویژگی‌های متوازی‌الاضلاع را دارد. بنابراین، مستطیل یک متوازی‌الاضلاع خاص است.

آیا مستطیل، ذوزنقه متساوی الساقین است؟

درس ۱۳، ریاضی ۸ (جلد ۱) مجموعه کتاب‌های درسی "پیوند دانش با زندگی" از انتشارات آموزش ویتنام، مستطیل تمام ویژگی‌های ذوزنقه متساوی‌الساقین را دارد. بنابراین، مستطیل شکل خاصی از ذوزنقه متساوی‌الساقین است.

(مصنوعی)

منبع: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html