आयत की परिधि की गणना करने का सूत्र क्या है?

आयत की परिभाषा

काइट बुक, गणित 3, खंड 1 में आयत को 4 समकोण, 2 बराबर लंबी भुजाओं और 2 बराबर छोटी भुजाओं वाली आकृति के रूप में परिभाषित किया गया है।

आयतों के गुण

एक आयत में समद्विबाहु समलम्ब और समांतर चतुर्भुज के सभी गुण होते हैं जैसे:

- विपरीत भुजाओं के जोड़े सदैव समान्तर एवं बराबर होते हैं।

- कोण बराबर और 90 डिग्री हैं।

- आयतों में विकर्णों और भुजाओं के मध्य-बिन्दुओं के माध्यम से समरूपता होती है।

आयत को पहचानने के संकेत

- तीन समकोण वाला चतुर्भुज एक आयत होता है।

- एक समकोण वाला समद्विबाहु समलम्ब एक आयत होता है।

- एक समकोण वाला समांतर चतुर्भुज एक आयत होता है।

- दो समान विकर्णों वाला फलक एक आयत होता है।

आयत की परिधि की गणना के लिए सूत्र

गणित 3 की पाठ्यपुस्तक के अनुसार, एक आयत की परिधि की गणना करने के लिए, हम लंबाई और चौड़ाई (माप की एक ही इकाई) लेते हैं और फिर 2 से गुणा करते हैं।

पी = (ए+बी) x 2

वहाँ पर

P आयत का परिमाप है।

a आयत की लंबाई है।

b आयत की चौड़ाई है।

उदाहरण के लिए: 6 सेमी लंबाई और 4 सेमी चौड़ाई वाले एक आयत का परिमाप ज्ञात कीजिए।

उत्तर: आयत का परिमाप P = (6+4) x 2 = 20 (सेमी) है।

आयतों और वर्गों की तुलना करें

मानदंड	आयत	वर्ग
किनारा	4 भुजाएँ, विपरीत भुजाओं के 2 जोड़े बराबर हैं	4 भुजाएँ, सभी 4 भुजाएँ बराबर हैं
कोना	4 समकोण	4 समकोण
विकर्ण	दो विकर्ण बराबर हैं, मध्य बिंदु पर प्रतिच्छेद करते हैं लेकिन लंबवत नहीं हैं	दो विकर्ण बराबर होते हैं, मध्य बिंदु पर प्रतिच्छेद करते हैं तथा एक दूसरे पर लंबवत होते हैं।
परिधि की गणना के लिए सूत्र	पी = (ए+बी) x 2	पी = 4ए
क्षेत्रफल की गणना के लिए सूत्र	एस = एक्सबी	एस = ए2

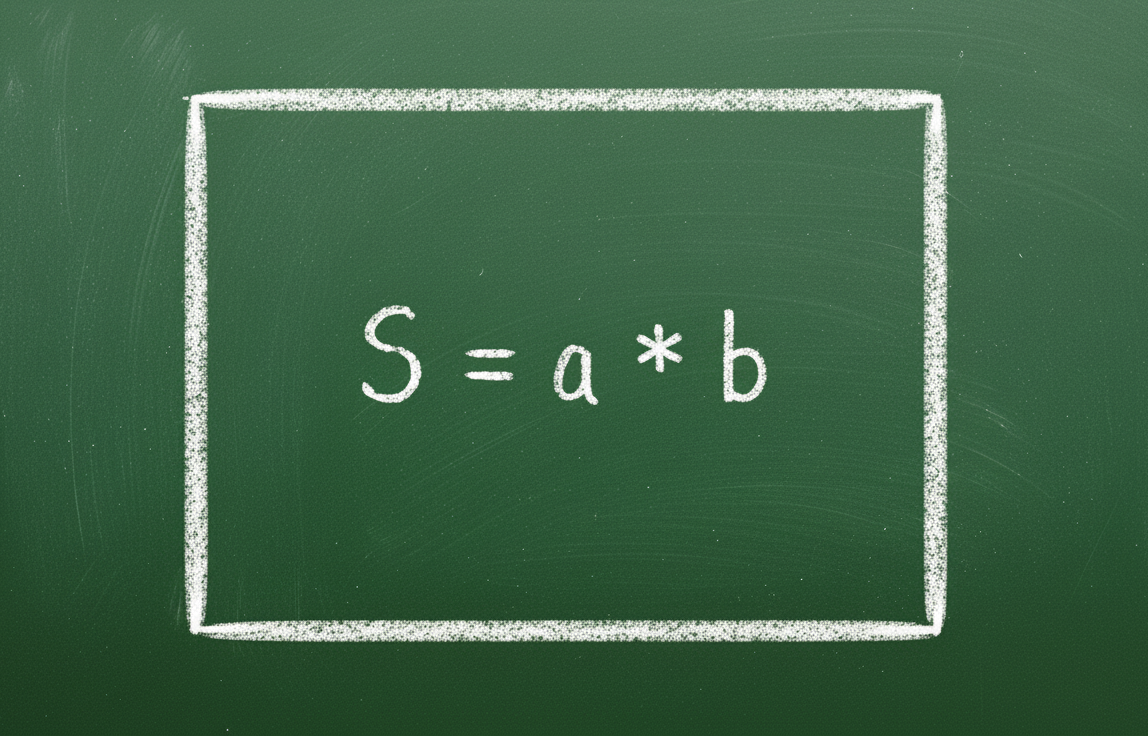
आयत के क्षेत्रफल की गणना करने का सूत्र आयत के क्षेत्रफल की गणना करने के लिए, लंबाई को चौड़ाई से गुणा करने के अलावा, एक पक्ष को जानने और विकर्ण या परिधि को जोड़ने पर भी गणना की जा सकती है।

स्रोत: https://vietnamnet.vn/cong-thuc-tinh-chu-vi-hinh-chu-nhat-la-gi-2452851.html