数学の試験が文学の試験だと思われ、ホーチミン市の10年生が泣いた

良いテスト、差別化されている、3科目で最低のスコア

ホーチミン市の10年生入学試験では、文学と外国語とともに数学が3科目ある。ホーチミン市は2015年から実践的な応用問題を取り入れた数学試験の改革を始めました。当初、数学の試験の問題は世論、生徒、教師の間で激しい反発を招いた。慣れてくると、試験の応用問題の数が増え、年によっては 4/7 問題を占め、残りの 2 問題はおなじみのもので、グラフ、ベトナム語の公式、方程式の解き方に関する基本問題と、平面幾何学に関する問題が 1 問あります。

応用数学の問題は長いものが多く、数学の試験用紙を持っていると文学だと思うことがあります。しかし、これらのレッスンは、公式や教科書、あるいは質問の種類に従わず、数学の目標に忠実で創造的であると考えられています。しかし、ホーチミン市での10年生の数学の試験も受験生を泣かせた。

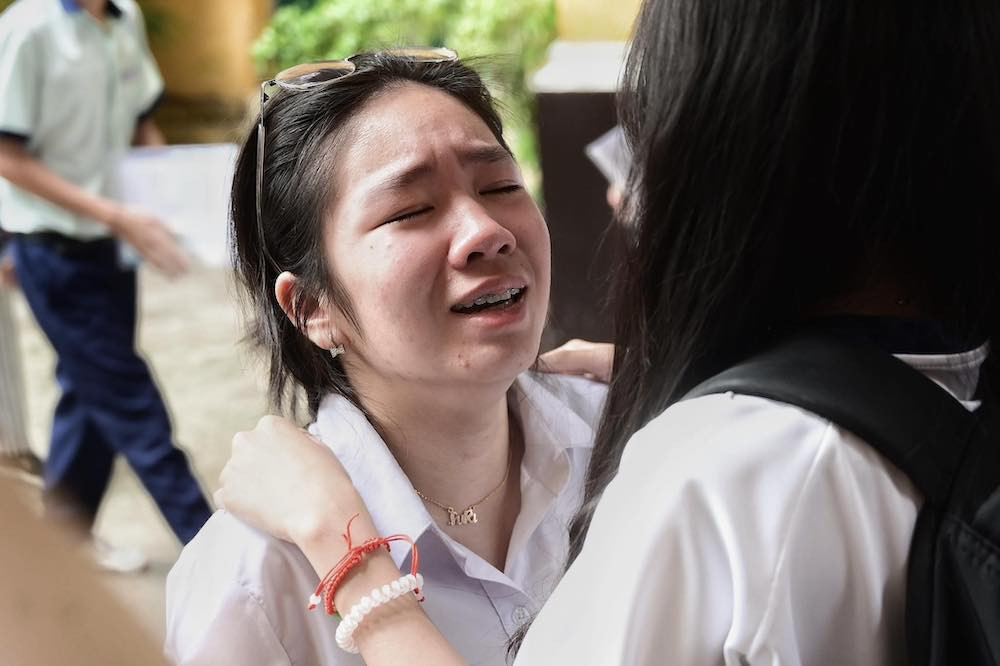
ホーチミン市の10年生数学受験生.jpg — ホーチミン市の10年生が数学のせいで泣いたことがありました。写真：*グエン・フエ*

典型的には、2024年に数学の試験室を出るときに、難しすぎるために多くの受験者が泣きました。当時ホーチミン市教育訓練局は、入学希望者の目的にかなうよう、試験問題には簡単なものと難しいものの差別化が必要であると説明した。卒業試験の目的である学生の知識を評価することとは異なり、10年生の入学試験では、より優秀で高い資格を持つ学生をトップ校に入学させ、より低い資格を持つ学生を中等学校および次にトップの学校に入学させるように分類する必要があります。

「10年生の入学試験実施前に、試験委員会は理解度、応用度、高度な応用度を判定するテストマトリックスを作成しました。2014年以降、ホーチミン市の数学科目では毎年、試験問題を解く際に生活知識を応用するレベルが引き上げられています。生徒は、学習した数学の知識を、設問に示された問題を解く際に応用するものとして選択しなければなりません」と、教育訓練局の担当者は述べた。

実際、2024年のホーチミン市の10年生の数学の試験の成績は明確に差別化されています。試験を受けた98,400人以上の受験者のうち、55,000人以上の数学のスコアが5未満で、そのうち123人の受験者は0.25でした。 142 名の候補者は 0.5 ポイントを獲得し、188 名の候補者は 0.75 ポイントしか獲得できず、256 名の候補者は 1 ポイントしか獲得できませんでした。数学では、10 点を獲得した受験者はわずか 49 人でした。 31人の受験者が9.75ポイントを獲得しました。 132人の受験者は9.5点を獲得しました。 123人の受験者が9.25ポイントを獲得しました。 276人の受験者が9ポイントを獲得しました。

2023年、数学試験を受けた95,952人の受験者のうち、44,126人が5点未満で、そのうち165人が0点でした。 134人の候補者0.25ポイント。数学の点数が1未満の生徒の数は809人です。2022年には92,074人の受験者が数学試験を受験し、そのうち41,775人が5未満の点数でした。

2025 年の試験でも、学んだ知識を応用して実際の問題を解決することが問われます。

2018年の一般教育プログラムによれば、2025年に行われる10年生の試験が最初の試験となる。数学の試験には、次の知識分野が含まれます: 幾何学と測定;数字と代数;統計と確率テスト内容は数学的能力を評価することを目的としています：数学的思考と推論。数学の問題を解く;数学モデリング

試験では、学生は学んだ知識を応用して実際の問題を解決することが求められます。暗記学習を避け、自習と創造性を奨励します。高校入学時に生徒が必要な知識とスキルを身に付けられるよう支援します。

トゥドゥック高校の数学教師、トラン・トゥアン・アン氏は、受験者が数学の試験で苦労する理由は、受験者が教師が指示した手順に従うだけで、練習問題の形で数学の問題を解くことに慣れているからだと語った。

一方、実践的な問題では、生徒は独自の解決プロセス、公式、方程式を構築する必要があるため、混乱してしまいます。一方、実践的な問題では、多くの場合、生徒は読解力を持ち、問題の仮説と要件を要約し、そこから変数、パラメータ、定数などのデータを特定し、それらの関係を数学的な言語で表現して構築する必要があります。

トゥアン・アン先生によると、実際の数学の問題を解くときに最も難しいのは問題の意味を理解することですが、生徒はそれを理解していないことが多いため、すぐに解くのが難しいとのこと。数学の本質には、一般的な計算、方程式の解決、証明などが含まれますが、古いタイプの質問ほど難しくはありません。

教師のトゥアン・アン氏によると、生徒たちがこうしたタイプの数学の問題で「泣く」ことを防ぐためには、まず教師が考え方を変える必要があるという。式の変換、式の値の計算、方程式の解決、不等式の解決、証明などの一般的な数学の知識は、数学学習の究極の目標ではありません。それは実際的な問題を解決するための強力なツールです。したがって、教師は、生徒に明確な手順を暗記させる演習形式での暗記学習を教えることを避ける必要があります。これにより、創造の自由が制限され、思考が制約され、「奇妙な」数学の問題に遭遇したときに生徒が混乱することになります。

一方、金融や統計などの実務分野の語彙を身近な実例を交えて授業に取り入れることで、問題理解、仮説の理解・まとめ、要件把握といった読解力を高めることも必要である。生徒は自然に学び、数学の問題を解く際に使用する数学的対象の定義と概念を理解する必要があります。使い方を知らないまま数式を暗記するのは避けましょう。

トゥアン・アン氏は、数学の学習は演習を解くことだけではなく、思考力を養い、正しく最適なものを見つけ、最も有益な決定を下すことにも役立つことを生徒たちに理解してもらうために、市の質問方法を支持しています。一方、10 年生の入学試験における実践的な数学の問題は、2018 年のプログラム目標に沿っており、難しい問題や機械的な変換が減り、応用性と実用性が向上しています。

出典: https://vietnamnet.vn/de-toan-cu-ngo-ngu-van-hoc-sinh-thi-lop-10-tphcm-tung-khoc-nuc-no-2396159.html