Formel zur Berechnung der Fläche eines Rechtecks

Was ist ein Rechteck?

Gemäß Lektion 13, Mathematik 8 (Band 1) der Lehrbuchreihe „Connecting knowledge with life“ des Vietnam Education Publishing House ist ein Rechteck ein Viereck mit vier rechten Winkeln.

Die Eigenschaften eines Rechtecks sind, dass es 2 parallele gegenüberliegende Seiten, 2 gleich lange gegenüberliegende Seiten, 2 gleich große gegenüberliegende Winkel und 2 gleich lange Diagonalen hat und sich in der Mitte jeder Seite schneidet.

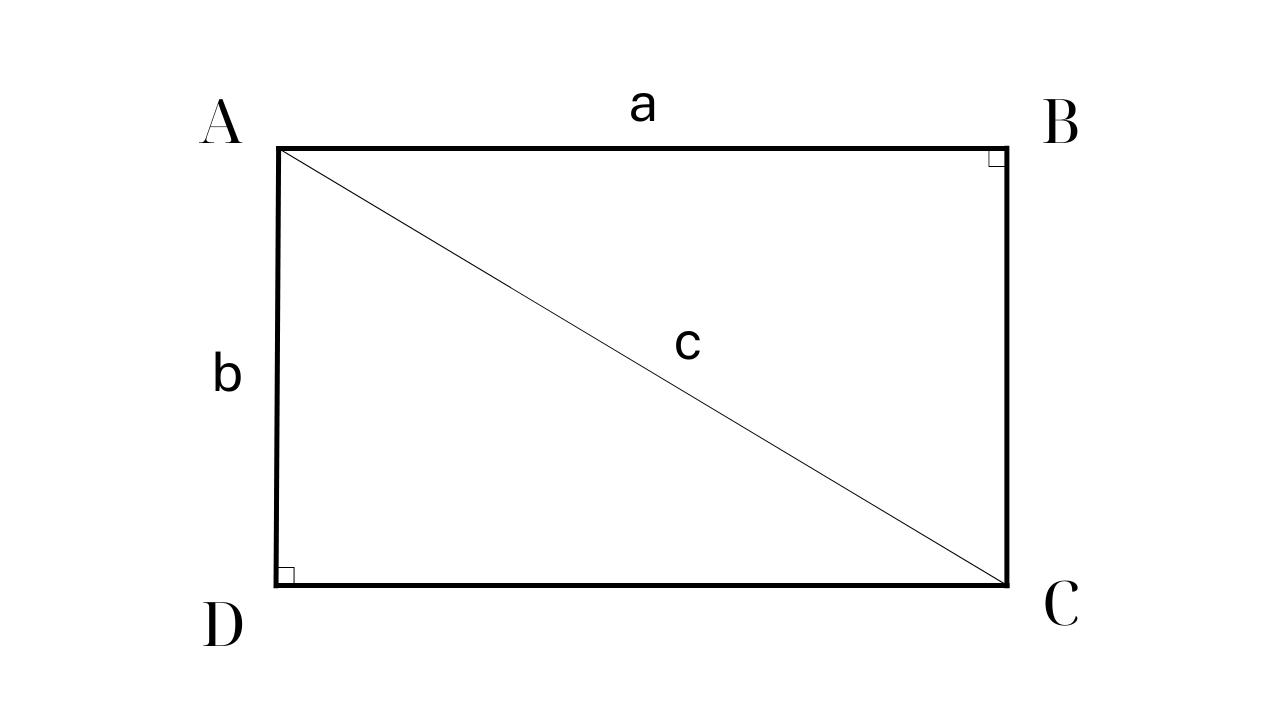
Formel zur Berechnung der Fläche eines Rechtecks

In Lektion 52, Mathematikbuch 3 (Band 2) der Lehrbuchreihe „Connecting knowledge with life“ des Vietnam Education Publishing House lautet die Formel zur Berechnung der Fläche eines Rechtecks Länge mal Breite (gleiche Maßeinheit).

S = axb

Dort drin:

S: Fläche des Rechtecks

a: Länge des Rechtecks

b: Die Breite des Rechtecks

Beispiel: Ein rechteckiges Holzbrett hat eine Breite von 5 cm und eine Länge von 15 cm. Berechnen Sie die Fläche dieses Holzbretts.

Antwort: Die Fläche des Holzbretts beträgt: S = 5 x 15 = 75 ( ^cm² )

Formel zur Berechnung der Fläche eines Rechtecks, wenn eine Seite und die Diagonale bekannt sind.

Um die Fläche eines Rechtecks zu berechnen, wenn seine Diagonale und eine Seite bekannt sind, muss man den Satz des Pythagoras mit der Grundformel für die Fläche kombinieren.

Schritt 1: Wenden Sie den Satz des Pythagoras auf das rechtwinklige Dreieck an, um die Länge der verbleibenden Seite zu berechnen.

Schritt 2: Wenden Sie die Formel zur Berechnung der Fläche eines Rechtecks an: S = axb

Beispiel: Ein Rechteck ABCD hat die Seitenlänge AD = 60 cm und die Diagonale AC = 100 cm. Berechnen Sie die Fläche von ABCD.

Antwort:

Schritt 1: Ermitteln Sie die verbleibende Seite des Rechtecks ABCD mithilfe des Satzes des Pythagoras im rechtwinkligen Dreieck.

Demnach: ^AC² = ^AB² + ^AD² => ^AB² = ^AC² - ^AD² = 10000 - 3600 = 6400 => AB = 80 cm

Schritt 2: Fläche von ABCD = AB x AD = 60 x 80 = 4800 ( ^cm² )

Formel zur Berechnung der Fläche eines Rechtecks bei bekanntem Umfang

Um die Fläche eines Rechtecks zu berechnen, wenn der Umfang bekannt ist, müssen Sie die Umfangsformel und die grundlegende Flächenformel kombinieren.

Schritt 1: Aus der Formel zur Berechnung des Umfangs eines Rechtecks P = (a+b) × 2, wobei P der Umfang, a die Länge und b die Breite des Rechtecks ist, ergibt sich a = (P/2) - b oder b = (P/2) - a

Schritt 2: Nachdem Sie a oder b ermittelt haben, wenden Sie die Formel zur Berechnung der Fläche eines Rechtecks an: S = axb

Zeichen zur Erkennung eines Rechtecks?

Laut Lektion 13 des Mathematikbuchs der Klasse 8 (Band 1) aus der Reihe „Wissen mit dem Leben verbinden“ des vietnamesischen Bildungsverlags lauten die Zeichen zur Erkennung eines Rechtecks:

- Ein Viereck hat 3 rechte Winkel (gemäß der Definition).

Das Parallelogramm hat 1 rechten Winkel

Ein Parallelogramm hat zwei gleich lange Diagonalen.

Ein gleichschenkliges Trapez hat einen rechten Winkel.

Ist ein Rechteck ein Parallelogramm?

Laut Lektion 13 des Mathematikbuchs der Klasse 8 (Band 1) aus der Reihe „Wissen mit dem Leben verbinden“ des vietnamesischen Bildungsverlags besitzt ein Rechteck alle Eigenschaften eines Parallelogramms. Daher ist ein Rechteck ein Spezialfall eines Parallelogramms.

Ist ein Rechteck ein gleichschenkliges Trapez?

In Lektion 13 des Mathematikbuchs der Reihe „Wissen mit dem Leben verbinden“ (Band 1) aus dem vietnamesischen Bildungsverlag heißt es, dass ein Rechteck alle Eigenschaften eines gleichschenkligen Trapezes besitzt. Daher ist ein Rechteck eine spezielle Form des gleichschenkligen Trapezes.

(Synthetik)

Quelle: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html