What is the Cosine Theorem? Cosine Theorem Formula in Triangle

The cosine theorem states the relationship between the lengths of three sides and an angle in a triangle.

Quick view:

• What is the Cosine Theorem?
• Cosine theorem formula in triangle
• When is the Cosine Theorem used?
• How is the Cosine Theorem different from the Pythagorean Theorem?
• Applications of the Cosine Theorem in practice
• Tips to quickly remember the Cosine Theorem formula

What is the Cosine Theorem?

The Cosine Rule (also known as the Law of Cosines) is an important theorem in triangle geometry, an extension and generalization of the Pythagorean theorem. This theorem establishes the relationship between one side of a triangle and the other two sides and the included angle.

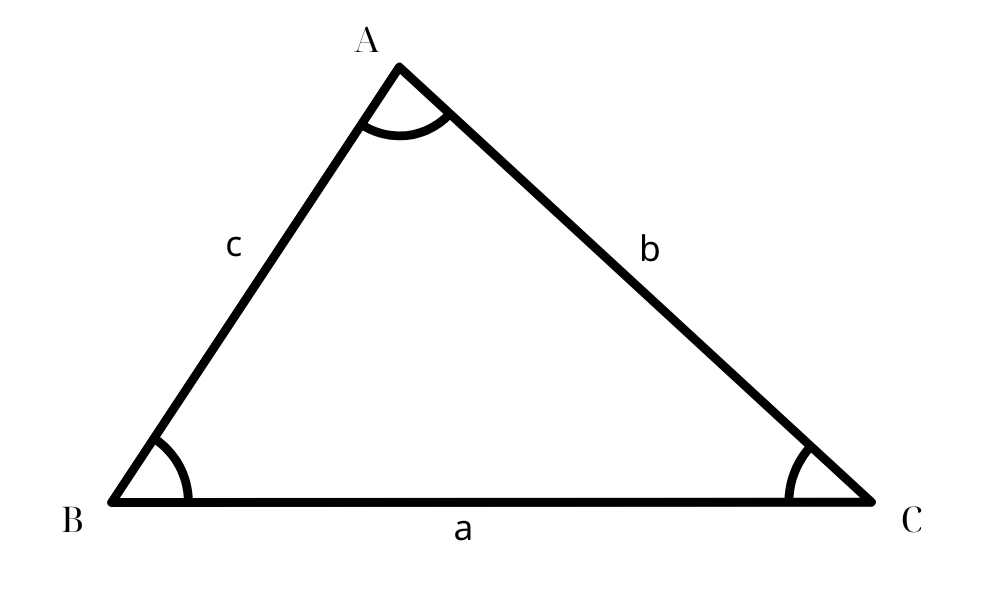
Cosine theorem formula in triangle

According to Math 10, volume 1, Canh Dieu series, the formula for the Cosine theorem in triangle ABC is:

a ² = b ² + c ² − 2 bc cos(A)

b ² = a ² + c ² − 2 ac cos(B)

c ² = a ² + b ² − 2 ab cos(C)

In there:

BC = a, CA = b, AB = c

A, B, C are the angles of the triangle

Consequences of the Cosine Theorem

When is the Cosine Theorem used?

The Cosine Theorem is used in two main cases.

- Knowing 2 sides and 1 angle between them: can calculate the remaining side.
- Knowing 3 sides of a triangle: can calculate one of the angles by transforming the formula to find the cosine of that angle.

How is the Cosine Theorem different from the Pythagorean Theorem?

Criteria	Cosine Theorem	Pythagorean Theorem
Scope of application	Every triangle	Right triangle only
General formula	a 2 =b 2 +c 2 −2bc cos(A)	c 2 = a 2 + b 2
Facts to know	2 sides and the angle between them or 3 sides	2 right angle sides
Intended use	Calculate the side or angle in any triangle	Calculate the remaining side in a right triangle
Relationship with each other	When angle A = 90 degrees, cos of angle 90 degrees = 0 so the formula becomes c 2 =a 2 +b 2	Is a special case of the Cosine Theorem
Practical applications	Measurement, surveying, force calculation, design of constructions with oblique angles	Basic geometry problem, measuring sides in a right triangle

Applications of the Cosine Theorem in practice

In practice, the Cosine Theorem can be applied in the following areas:

- Mathematics & Education : solve complex triangle problems, calculate sides or angles in plane geometry.
- Geography & Geodesy: measure the distance between two points when knowing the length and angle.
- Physics: calculate the resultant force of two non-perpendicular force vectors.
- Construction - Engineering: used in calculating the design of works with oblique angles and sloping roofs.

Tips to quickly remember the Cosine Theorem formula

The formula for the Cosine Theorem is similar to the Pythagorean Theorem. You just need to remember: “the square of the opposite side = the sum of the squares of the two adjacent sides - 2 times the product of the two adjacent sides times the cosine of the included angle”.

Source: https://vietnamnet.vn/dinh-ly-cosine-la-gi-cong-thuc-dinh-ly-cosine-trong-tam-giac-2452865.html