Formel for å beregne arealet av et rektangel

For å beregne arealet av et rektangel, i tillegg til å multiplisere lengden med bredden, kan du også beregne det ved å kjenne én side og legge til diagonalen eller omkretsen.

VietNamNet•26/09/2025

Hva er et rektangel?

I følge leksjon 13, matematikk 8 (bind 1) i lærebokserien «Connecting Knowledge with Life» utgitt av Vietnam Education Publishing House, er et rektangel definert som en firkant med fire rette vinkler.

Egenskapene til et rektangel er at det har to parallelle motstående sider, to like motstående sider, to like motstående vinkler og to like diagonaler som skjærer hverandre i midtpunktet på hver diagonal.

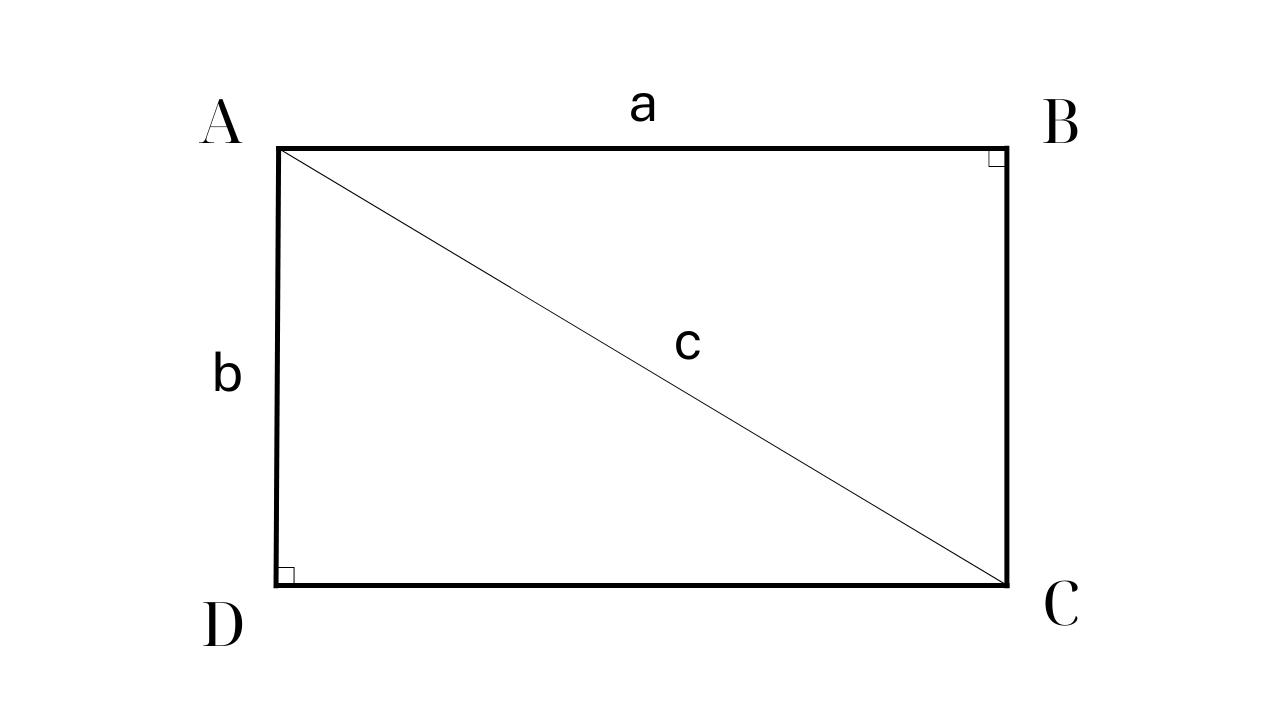
Formel for å beregne arealet av et rektangel

I leksjon 52 i læreboken Matematikk 3 (bind 2) i serien «Connecting Knowledge with Life», utgitt av Vietnam Education Publishing House, er formelen for å beregne arealet av et rektangel lengden multiplisert med bredden (ved bruk av samme måleenhet).

S = aksb

Der inne:

S: Arealet av rektangelet

a: Lengden på rektangelet

b: Bredden på rektangelet

Eksempel: Et rektangulært trestykke har en bredde på 5 cm og en lengde på 15 cm. Beregn arealet av trestykket.

Svar: Arealet av treplanken er: S = 5 x 15 = 75 ( ^cm² )

Formel for å beregne arealet av et rektangel når én side og diagonalen er kjent.

For å beregne arealet av et rektangel gitt diagonalen og den ene siden, må du kombinere Pythagoras' læresetning med den grunnleggende arealformelen.

Trinn 1: Bruk Pythagoras' læresetning på den rettvinklede trekanten for å beregne lengden på den gjenværende siden.

Trinn 2: Bruk formelen for å beregne arealet av et rektangel: S = axb

Eksempel: Et rektangel ABCD har AD = 60 cm og diagonalen AC = 100 cm. Beregn arealet av ABCD.

Svare:

Trinn 1: Finn den gjenværende siden av rektangelet ABCD ved hjelp av Pythagoras' læresetning i en rettvinklet trekant.

Følgelig: ^AC² = ^AB² + ^AD² => ^AB² = ^AC² - ^AD² = 10000 - 3600 = 6400 => AB = 80 (cm)

Trinn 2: Areal av ABCD = AB x AD = 60 x 80 = 4800 ( ^cm² )

Formel for å beregne arealet av et rektangel når omkretsen er kjent.

For å beregne arealet av et rektangel når omkretsen er kjent, må du kombinere omkretsformelen og den grunnleggende arealformelen.

Trinn 1: Fra formelen for å beregne omkretsen av et rektangel, som er P = (a+b) x 2, hvor P er omkretsen, a er lengden og b er bredden på rektangelet, har vi a = (P/2) - b eller b = (P/2) - a

Trinn 2: Etter å ha funnet a eller b, bruk formelen for å beregne arealet av et rektangel: S = axb

Hvordan identifisere et rektangel?

I følge leksjon 13, matematikk 8 (bind 1) i lærebokserien «Connecting Knowledge with Life», utgitt av Vietnam Education Publishing House, er de identifiserende egenskapene til et rektangel:

- En firkant har 3 rette vinkler (basert på definisjonen)

- Et parallellogram har én rett vinkel.

- Et parallellogram har to like diagonaler.

- En likebenet trapes har en rett vinkel.

Er et rektangel et parallellogram?

I følge leksjon 13, matematikk 8 (bind 1) i lærebokserien «Connecting Knowledge with Life», utgitt av Vietnam Education Publishing House, har et rektangel alle egenskapene til et parallellogram. Derfor er et rektangel en spesiell type parallellogram.

Er et rektangel en likebenet trapes?

Leksjon 13, matematikk 8 (bind 1) – en del av lærebokserien «Connecting Knowledge with Life» utgitt av Vietnam Education Publishing House, sier at et rektangel har alle egenskapene til en likebent trapes. Derfor er et rektangel en spesiell type likebent trapes.

(Syntetisk)

Kilde: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html