کتاب بادبادک، ریاضی ۳، جلد ۱، مستطیل را به عنوان شکلی با ۴ زاویه قائمه، ۲ ضلع بلند مساوی و ۲ ضلع کوتاه مساوی تعریف میکند.

یک مستطیل تمام خواص یک ذوزنقه متساوی الساقین و یک متوازی الاضلاع را دارد، مانند:
- جفت اضلاع روبرو همیشه موازی و مساوی هستند.
- زاویه ها مساوی و ۹۰ درجه هستند.
- مستطیلها از طریق قطرها و از طریق نقاط میانی اضلاع، تقارن دارند.
- هر چهارضلعی که سه زاویه قائمه داشته باشد، مستطیل است.
- ذوزنقه متساوی الساقین با یک زاویه قائمه، مستطیل است.
- متوازی الاضلاعی که یک زاویه قائمه داشته باشد، مستطیل است.
- وجهی که دو قطر مساوی داشته باشد، مستطیل است.
طبق کتاب درسی ریاضی ۳، برای محاسبه محیط مستطیل، طول را به علاوه عرض (همان واحد اندازه گیری) در نظر می گیریم و سپس در ۲ ضرب می کنیم.
| پ = (الف+ب) ضربدر ۲ |
در آنجا
P محیط مستطیل است.
a طول مستطیل است.
b عرض مستطیل است.

مثال: محیط مستطیلی به طول ۶ سانتیمتر و عرض ۴ سانتیمتر را محاسبه کنید.
پاسخ: محیط مستطیل P = (6+4) x 2 = 20 (سانتیمتر) است.
مقایسه مستطیل و مربع
| معیارها | مستطیل | مربع |
|---|---|---|
| لبه | ۴ ضلع، ۲ جفت از اضلاع روبرو با هم برابرند | ۴ ضلع، هر ۴ ضلع با هم برابرند |
| گوشه | ۴ زاویه قائمه | ۴ زاویه قائمه |
| مورب | دو قطر با هم مساوی هستند، در نقطه وسط یکدیگر را قطع میکنند اما بر هم عمود نیستند | دو قطر با هم مساوی هستند، در نقطه وسط یکدیگر را قطع میکنند و بر هم عمودند. |
| فرمول محاسبه محیط | پ = (الف+ب) ضربدر ۲ | پ = 4a |
| فرمول محاسبه مساحت | S = axb | س = a2 |
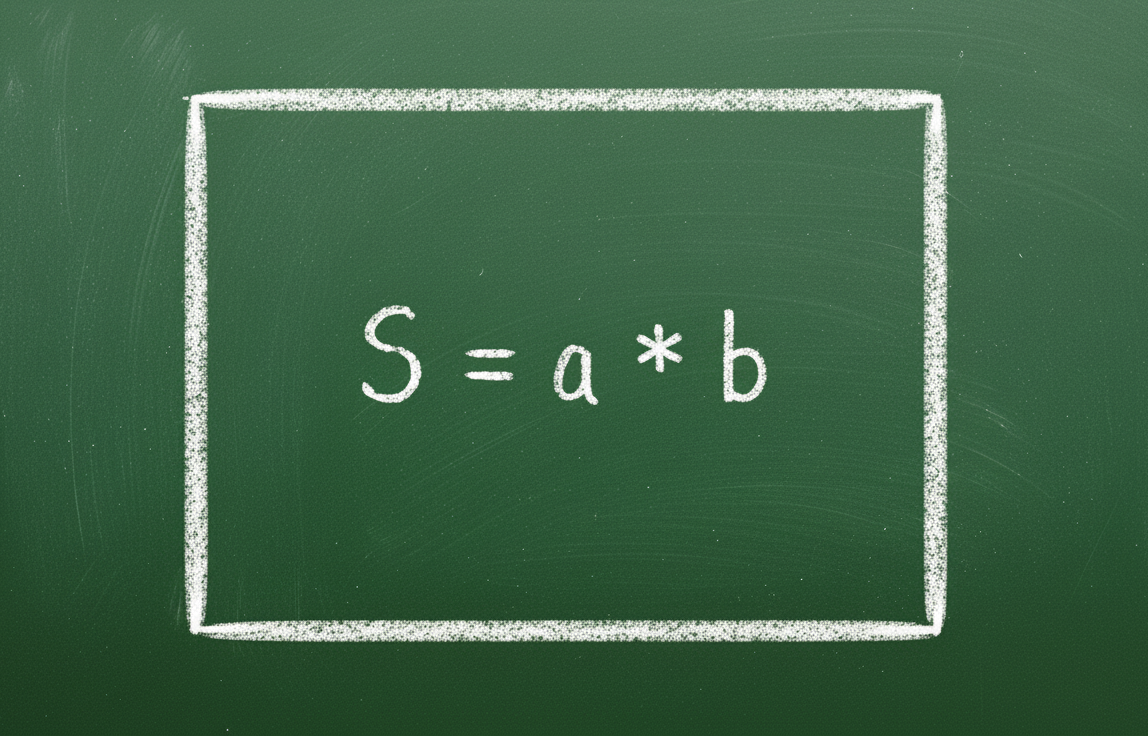
منبع: https://vietnamnet.vn/cong-thuc-tinh-chu-vi-hinh-chu-nhat-la-gi-2452851.html



![[عکس] جمعآوری زباله، کاشت بذر سبز](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760786475497_ndo_br_1-jpg.webp)

![[عکس] دبیرکل تو لام در نود و پنجمین سالگرد روز سنتی دفتر مرکزی حزب شرکت میکند](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/18/1760784671836_a1-bnd-4476-1940-jpg.webp)

![[عکس] مراسم اختتامیه هجدهمین کنگره کمیته حزب هانوی](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/10/17/1760704850107_ndo_br_1-jpg.webp)


























































































نظر (0)