Le problème de trouver le chat derrière la porte

Ce problème de mathématiques de niveau CM2 demande au lecteur de calculer le nombre de portes à ouvrir pour trouver le chat, sachant qu'après chaque ouverture d'une porte vide, le chat se déplacera vers une autre porte.

Sujet:

Un couloir rectiligne comporte cinq portes sur un côté. Derrière l'une d'elles se cache un chat. Votre mission est de trouver le chat en ouvrant la bonne porte. Vous ne pouvez ouvrir qu'une seule porte par jour. Si le chat est là, vous avez gagné.

Si le chat n'est pas là, la porte se fermera et vous devrez attendre le lendemain pour la rouvrir. Le chat bouge constamment et chaque nuit, il change de porte. Il s'agit de la porte située à gauche ou à droite de celle où il se trouve actuellement.

Combien de jours vous faut-il pour être sûr de retrouver le chat ?

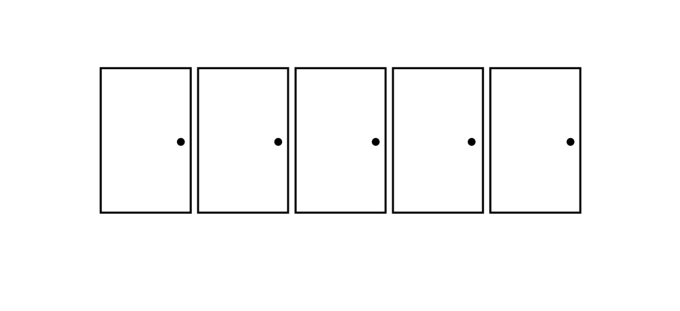
Le problème consiste à trouver une stratégie permettant d'attraper le chat en un nombre de jours fixe, quelle que soit la porte derrière laquelle il se cache au départ et où il se déplace la nuit. La clé de la solution est de commencer avec un petit nombre de portes, de repérer la régularité de ses déplacements, puis d'augmenter progressivement ce nombre.

Prenons l'exemple d'une maison à trois portes. Si vous ouvrez la porte du milieu deux jours de suite, vous êtes certain d'attraper le chat, car s'il n'est pas derrière cette porte le premier jour, il est forcément derrière l'une des deux portes latérales. Et s'il est derrière l'une de ces portes le premier jour, il n'aura d'autre choix que de se déplacer vers la porte du milieu le deuxième jour.

S'il y a quatre portes, vous pouvez attraper le chat en quatre jours. L'explication se trouve dans la réponse ci-dessous, mais avant cela, essayez de la comprendre par vous-même. N'oubliez pas : le chat se déplace uniquement vers la porte immédiatement à sa droite ou à sa gauche et peut retourner à celle derrière laquelle il se trouvait auparavant. Vous serez certainement ravi(e) en trouvant l'explication.

>>>Réponse

Vo Quoc Ba Can

Professeur de mathématiques, École Archimède de Hanoï

Lien source: https://vnexpress.net/bai-toan-tim-con-meo-sau-canh-cua-4604654.html