«Проблема з окропом» на іспиті 10-го класу викликає суперечки

Хошимін: Проблема кипіння води на іспиті з математики у 10-му класі викликала суперечки, оскільки її вважали нелогічною в реальності та неправильною з точки зору знань з фізики.

6 та 7 червня майже 96 000 кандидатів складали іспити з літератури, іноземної мови та математики, щоб поборотися за місце у 10-му класі державних шкіл Хошиміна. Вчителі зазначили, що іспит з математики мав таку ж структуру та складність, як і минулого року. Іспит містив 5 практичних завдань, від питання 3 до питання 7.

Після закінчення іспиту пан Май Ван Тук, викладач фізики у Вищій школі природничих наук Ханойського національного університету, заявив, що питання 5 на іспиті з математики для 10-го класу в Хошиміні містить правило, якого насправді не існує та є неправильним за своєю природою.

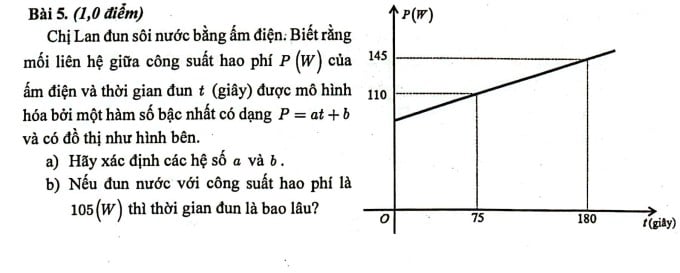
Запитання 5 на вступному іспиті з математики для 10-го класу державної школи в Хошиміні.

Зокрема, процес перетворення енергії при кипінні води розраховується з моменту ввімкнення вимикача (при t = 0); електрична енергія перетворюється на теплову, що призводить до нагрівання нагрівального дроту (якщо в чайнику використовується нагрівальний дріт). Нагрівальний дріт має вищу температуру, ніж вода в чайнику, і передає тепло воді, вода передає тепло чайнику, і потрібен певний час, щоб тепло втратило в навколишнє середовище. Тепловтратна здатність у навколишнє середовище залежить головним чином від площі контакту чайника з навколишнім середовищем та різниці температур між температурою чайника та навколишнього середовища (тепловтратна здатність також залежить від рівня циркуляції повітря або вітру в місці нагрівання). Коли тепловтратна здатність чайника у навколишнє середовище дорівнює потужності, отриманій нагрівальним дротом, температура води більше не підвищуватиметься.

Вчитель Тук навів приклад нагрівального дроту потужністю 1000 Вт. Якщо воду кип'ятити в 2-літровому чайнику, вона може кипіти, але якщо цей нагрівальний дріт забезпечує тепло для великого акваріума, вода може нагріватися лише від 10 градусів Цельсія до 30 градусів Цельсія, тоді температура більше не підвищуватиметься. У цей час втрати потужності постійні та дорівнюють споживаній потужності нагрівального дроту чайника. Отже, у завданні 5 наведено втрати потужності згідно з правилом P = at + b, тобто t = 0, що має втрати потужності 85 Вт, і втрати потужності постійно зростають, що є неправильним. Вчитель також вважає, що запитання «Якщо воду кип'ятять з втратами потужності 105 Вт, скільки часу знадобиться, щоб вона закипіла» є неправильним. Якщо ми припустимо, що існує нелогічне правило, як наводить автор, нам потрібно запитати: Обчисліть час кипіння, доки втрати потужності не становитимуть 105 Вт.

З огляду на ці аргументи, пан Тук запропонував Департаменту освіти та навчання міста Хошпітал-Сіті скоригувати відповідь на запитання 5, щоб забезпечити справедливість для кандидатів. Цей вчитель вважає, що учні, які добре знаються на фізиці, можуть не впоратися з запитанням 5, якщо дані в завданні занадто дивні.

Тим часом, пан Лам Ву Конг Чінь, вчитель математики у середній школі Нгуєн Ду в місті Хошимін, сказав, що якщо враховувати знання з фізики та реальність, то дані у питанні 5 не є обґрунтованими та логічними. Однак, якщо питання є лише опитуванням, синтезом та формулою прогнозування, а не точною фізичною формулою, воно все одно прийнятне.

Пан Чін навів приклад оцінки приросту населення. За його словами, це проблема, яка не має абсолютно точної формули, проте експерти все ж застосовують формулу відповідно до певних правил і фактів для прогнозування та оцінки майбутньої чисельності населення.

«Якщо студенти застосовують математичні знання, вони все одно можуть розв’язати задачу звичайним чином. Ця помилка не впливає на результати тестування кандидатів», – сказав пан Чінх.

Пані Нгуєн Тьєн Туй, вчителька математики середньої школи Ха Хьюй Тап, Хошимін, зазначила, що завдання 5 є задачею на функції першого ступеня. У завданні наведено формулу для функції першого ступеня з чіткими формулами для кожної величини та одиниці вимірювання, а також графічними ілюстраціями, щоб учні могли розв'язати її як зазвичай.

Кандидати розмовляють після іспиту з математики, ранок 7 червня. Фото: Ле Нгуєн — Кандидати розмовляють після іспиту з математики, ранок 7 червня. Фото *: Ле Нгуєн*

9 червня Департамент освіти та навчання міста Хошимін оголосив, що питання 5 вступного іспиту з математики для 10-го класу стосується реального явища кипіння води в електричному чайнику. Цей процес опитування є лише коротким етапом процесу кипіння води, і час початку опитування (t = 0) не є часом початку процесу кипіння води.

За допомогою даних, отриманих у цьому процесі, математично це можна описати як креслення та за допомогою функції, яку студенти вивчили в програмі. Отже, маючи математичні знання та вміння (функція першого ступеня, графік функції першого ступеня, точки на графіку, система рівнянь першого ступеня з двома невідомими, обчислення), студенти можуть розв'язати вимоги, поставлені в задачі.

«У випадках, коли учні мають рішення, що відрізняються від інструкцій щодо оцінювання, але є обґрунтованими, вони будуть розглянуті та оцінені», – заявили в Департаменті інформації.

Минулого року близько 45% кандидатів, які складали вступний іспит до 10-го класу в Хошиміні, отримали бали з математики нижче середнього.

Цього року в Хошиміні близько 96 000 учнів складають вступний іспит до 10-го класу. Загальна квота для 108 державних середніх шкіл міста становить 77 300 осіб, а рівень вступу – близько 80%. Департамент освіти та навчання повідомив, що результати іспитів будуть оголошені 20 червня.

Ле Нгуєн

Посилання на джерело