Что такое прямоугольник?
Согласно Уроку 13, Математика 8 (Том 1) серии учебников «Связь знаний с жизнью» издательства Vietnam Education Publishing House, прямоугольник определяется как четырехугольник с 4 прямыми углами.
Свойства прямоугольника таковы, что он имеет 2 параллельные противолежащие стороны, 2 равные противолежащие стороны, 2 равные противолежащие углы, 2 равные диагонали и пересекается в середине каждой линии.
Формула для вычисления площади прямоугольника
В уроке 52, математика, книга 3 (том 2) учебника серии «Связь знаний с жизнью» издательства Vietnam Education House, формула для вычисления площади прямоугольника — длина, умноженная на ширину (единая единица измерения).
| S = axb |
Там:
S: Площадь прямоугольника
а: Длина прямоугольника
b: Ширина прямоугольника
Например: прямоугольная деревянная доска имеет ширину 5 см и длину 15 см. Рассчитайте площадь этой деревянной доски.
Ответ: Площадь деревянной доски составляет: S = 5 x 15 = 75 ( см² )
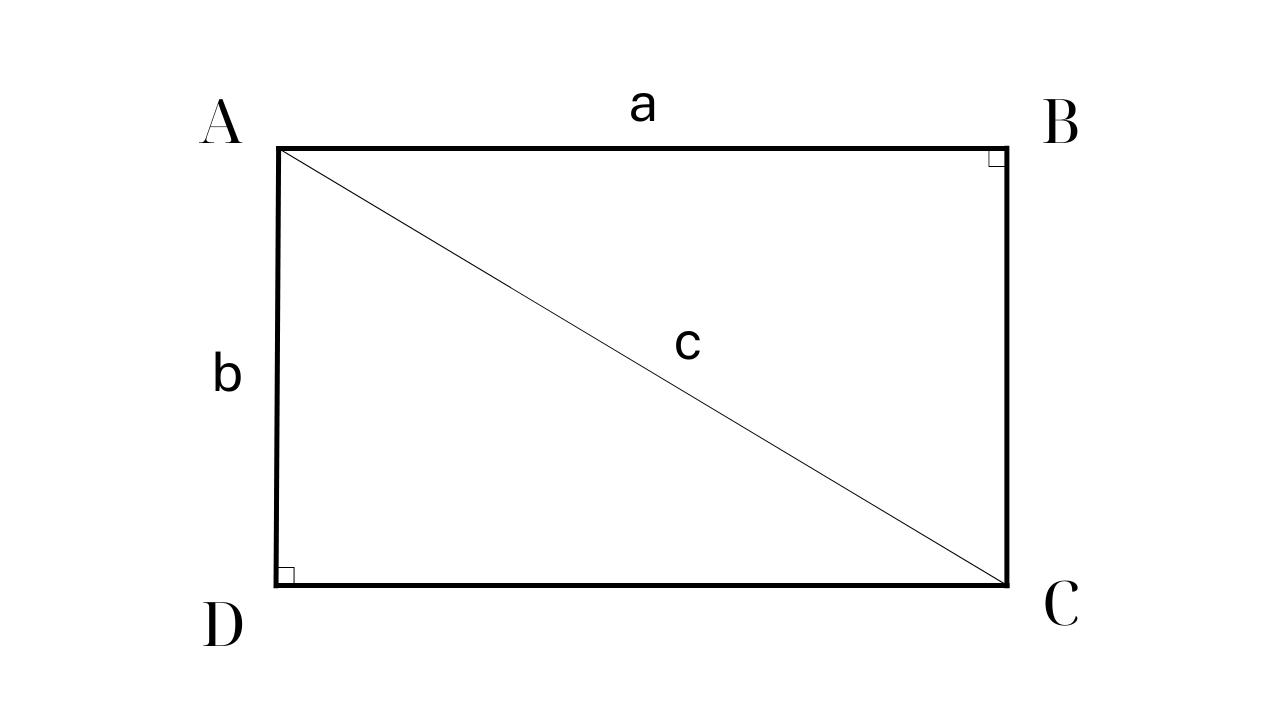
Формула для вычисления площади прямоугольника, если известны одна сторона и диагональ.
Для вычисления площади прямоугольника, зная его диагональ и одну из сторон, необходимо объединить теорему Пифагора с основной формулой площади.
Шаг 1: Примените теорему Пифагора к прямоугольному треугольнику, чтобы вычислить длину оставшейся стороны.
Шаг 2: Примените формулу для вычисления площади прямоугольника: S = axb
Пример: Прямоугольник ABCD имеет длину AD = 60 см и диагональ AC = 100 см. Вычислите площадь прямоугольника ABCD.
Отвечать:
Шаг 1: Найдите оставшуюся сторону прямоугольника ABCD, используя теорему Пифагора в прямоугольном треугольнике.
Соответственно: AC2 = AB2 + AD2 => AB2 = AC2 - AD2 = 10000 - 3600 = 6400 => AB = 80 (см)
Шаг 2: Площадь ABCD = AB x AD = 60 x 80 = 4800 ( см² )
Формула вычисления площади прямоугольника, если известен его периметр.
Для вычисления площади прямоугольника, если известен его периметр, необходимо объединить формулу расчета периметра и основную формулу расчета площади.
Шаг 1: Из формулы для вычисления периметра прямоугольника P = (a+b) x 2, где P — периметр, a — длина, b — ширина прямоугольника, получаем a = (P/2) - b или b = (P/2) - a
Шаг 2: Найдя a или b, примените формулу для вычисления площади прямоугольника: S = axb
Признаки, распознающие прямоугольник?
Согласно уроку 13 учебника по математике 8 (том 1) серии «Связь знаний с жизнью» издательства Vietnam Education Publishing House, признаки, по которым можно распознать прямоугольник, следующие:
- Четырехугольник имеет 3 прямых угла (согласно определению)
- Параллелограмм имеет 1 прямой угол.
- Параллелограмм имеет две равные диагонали.
- Равнобедренная трапеция имеет один прямой угол.
Является ли прямоугольник параллелограммом?
Согласно уроку 13 учебника по математике 8 (том 1) серии «Связь знаний с жизнью» издательства Vietnam Education Publishing, прямоугольник обладает всеми свойствами параллелограмма. Следовательно, прямоугольник является его особым параллелограммом.
Является ли прямоугольник равнобедренной трапецией?
Урок 13, Математика 8 (Том 1) из серии учебников «Связь знаний с жизнью» издательства Vietnam Education, прямоугольник обладает всеми свойствами равнобедренной трапеции. Следовательно, прямоугольник является частным случаем равнобедренной трапеции.
(Синтетический)
Источник: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html






![[Фото] Очаровательный пейзаж кленового леса в провинции Куангчи.](/_next/image?url=https%3A%2F%2Fvphoto.vietnam.vn%2Fthumb%2F1200x675%2Fvietnam%2Fresource%2FIMAGE%2F2025%2F12%2F10%2F1765353233198_lan09046-jpg.webp&w=3840&q=75)
![[Фото] Осмотрите военный корабль ВМС США USS Robert Smalls.](/_next/image?url=https%3A%2F%2Fvphoto.vietnam.vn%2Fthumb%2F1200x675%2Fvietnam%2Fresource%2FIMAGE%2F2025%2F12%2F10%2F1765341533272_11212121-8303-jpg.webp&w=3840&q=75)






















![[Видео] Ремесло создания народных картин Донг Хо внесено ЮНЕСКО в Список ремесел, нуждающихся в срочной охране.](https://vphoto.vietnam.vn/thumb/402x226/vietnam/resource/IMAGE/2025/12/10/1765350246533_tranh-dong-ho-734-jpg.webp)









































































Комментарий (0)