ما هو المستطيل؟
وفقًا للدرس 13، الرياضيات 8 (المجلد 1) من سلسلة الكتب المدرسية "ربط المعرفة بالحياة" التي نشرتها دار النشر التعليمية الفيتنامية، يتم تعريف المستطيل على أنه شكل رباعي ذو أربع زوايا قائمة.
خصائص المستطيل هي أنه يحتوي على ضلعين متقابلين متوازيين، وضلعين متقابلين متساويين، وزاويتين متقابلتين متساويتين، وقطرين متساويين يتقاطعان عند منتصف كل قطر.
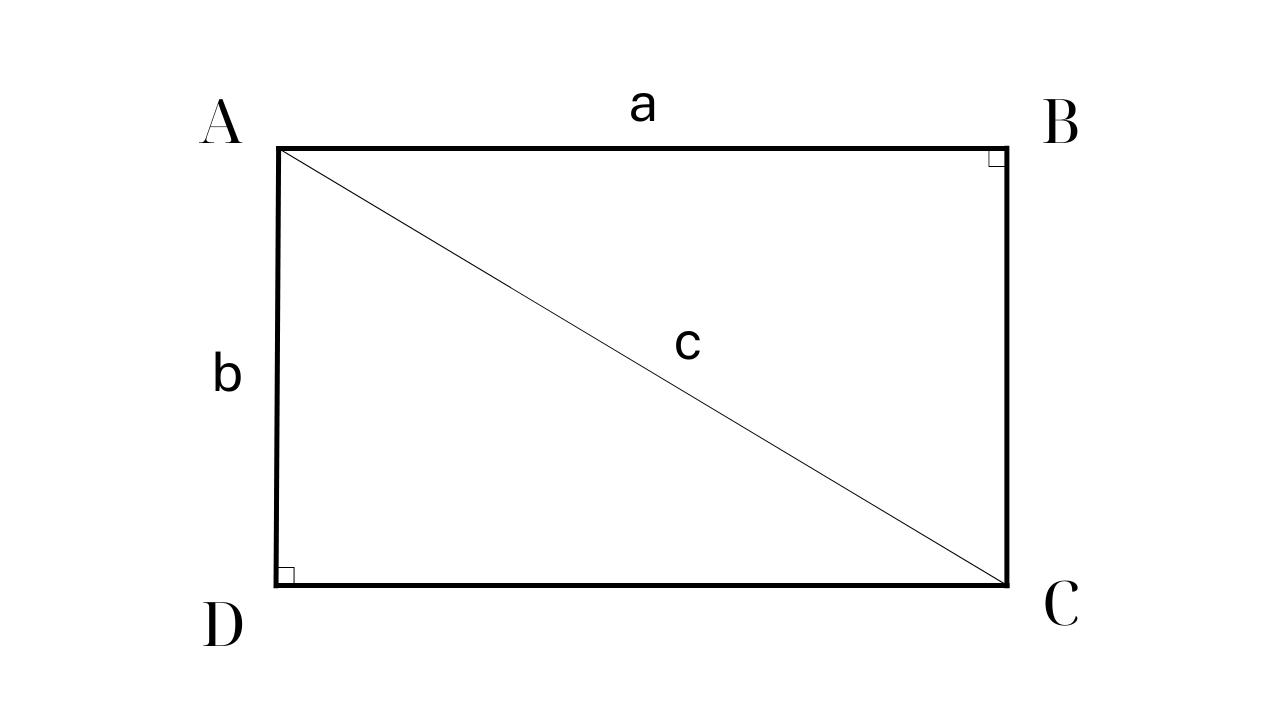
صيغة حساب مساحة المستطيل
في الدرس 52 من كتاب الرياضيات 3 (المجلد 2) في سلسلة "ربط المعرفة بالحياة" التي نشرتها دار النشر التعليمية الفيتنامية، فإن صيغة حساب مساحة المستطيل هي الطول مضروبًا في العرض (باستخدام نفس وحدة القياس).
| س = محور ب |
هناك:
S: مساحة المستطيل
أ: طول المستطيل
ب: عرض المستطيل
مثال: قطعة خشب مستطيلة الشكل عرضها 5 سم وطولها 15 سم. احسب مساحة قطعة الخشب.
الإجابة: مساحة اللوح الخشبي هي: S = 5 × 15 = 75 ( سم² )
صيغة لحساب مساحة المستطيل عندما يكون أحد أضلاعه وقطره معروفين.
لحساب مساحة مستطيل بمعلومية قطره وأحد أضلاعه، تحتاج إلى الجمع بين نظرية فيثاغورس وصيغة المساحة الأساسية.
الخطوة 1: تطبيق نظرية فيثاغورس على المثلث القائم لحساب طول الضلع المتبقي.
الخطوة الثانية: تطبيق صيغة حساب مساحة المستطيل: S = axb
مثال: مستطيل ABCD طول ضلعه AD = 60 سم وقطره AC = 100 سم. احسب مساحة المستطيل ABCD.
إجابة:
الخطوة 1: إيجاد الضلع المتبقي من المستطيل ABCD باستخدام نظرية فيثاغورس في المثلث القائم الزاوية.
وبناءً على ذلك: AC² = AB² + AD² => AB² = AC² - AD² = 10000 - 3600 = 6400 => AB = 80 (سم)
الخطوة 2: مساحة الشكل ABCD = AB × AD = 60 × 80 = 4800 ( سم² )
صيغة لحساب مساحة المستطيل عندما يكون المحيط معروفًا.
لحساب مساحة المستطيل عندما يكون المحيط معروفًا، تحتاج إلى الجمع بين صيغة المحيط وصيغة المساحة الأساسية.
الخطوة 1: من صيغة حساب محيط المستطيل، وهي P = (a + b) × 2، حيث P هو المحيط، وa هو الطول، وb هو عرض المستطيل، نحصل على: a = (P/2) - b أو b = (P/2) - a
الخطوة الثانية: بعد إيجاد قيمة a أو b، يتم تطبيق صيغة حساب مساحة المستطيل: S = axb
كيف يمكن تحديد شكل المستطيل؟
وفقًا للدرس 13، الرياضيات 8 (المجلد 1) من سلسلة كتب "ربط المعرفة بالحياة" التي نشرتها دار النشر التعليمية الفيتنامية، فإن الخصائص المميزة للمستطيل هي:
- الشكل الرباعي له 3 زوايا قائمة (بناءً على التعريف)
- متوازي الأضلاع له زاوية قائمة واحدة.
- متوازي الأضلاع له قطران متساويان.
- شبه المنحرف متساوي الساقين له زاوية قائمة.
هل المستطيل متوازي أضلاع؟
بحسب الدرس الثالث عشر من كتاب الرياضيات للصف الثامن (المجلد الأول) من سلسلة كتب "ربط المعرفة بالحياة" الصادرة عن دار النشر التعليمية الفيتنامية، فإن المستطيل يمتلك جميع خصائص متوازي الأضلاع. لذا، يُعد المستطيل نوعًا خاصًا من متوازي الأضلاع.
هل المستطيل هو شبه منحرف متساوي الساقين؟
الدرس الثالث عشر، الرياضيات للصف الثامن (المجلد الأول) - وهو جزء من سلسلة كتب "ربط المعرفة بالحياة" الصادرة عن دار النشر التعليمية الفيتنامية - ينص على أن المستطيل يمتلك جميع خصائص شبه المنحرف متساوي الساقين. لذلك، يُعد المستطيل نوعًا خاصًا من شبه المنحرف متساوي الساقين.
(اصطناعي)
المصدر: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html




![[صورة] استكشف السفينة الحربية يو إس إس روبرت سمولز التابعة للبحرية الأمريكية](/_next/image?url=https%3A%2F%2Fvphoto.vietnam.vn%2Fthumb%2F1200x675%2Fvietnam%2Fresource%2FIMAGE%2F2025%2F12%2F10%2F1765341533272_11212121-8303-jpg.webp&w=3840&q=75)


![[صورة] المناظر الخلابة لغابة القيقب العطرة في كوانغ تري](/_next/image?url=https%3A%2F%2Fvphoto.vietnam.vn%2Fthumb%2F1200x675%2Fvietnam%2Fresource%2FIMAGE%2F2025%2F12%2F10%2F1765353233198_lan09046-jpg.webp&w=3840&q=75)
























![[فيديو] تم إدراج حرفة صنع لوحات دونغ هو الشعبية من قبل اليونسكو في قائمة الحرف التي تحتاج إلى حماية عاجلة.](https://vphoto.vietnam.vn/thumb/402x226/vietnam/resource/IMAGE/2025/12/10/1765350246533_tranh-dong-ho-734-jpg.webp)









































































تعليق (0)