Vzorec pro výpočet plochy obdélníku

Co je to obdélník?

Podle 13. lekce, matematika 8 (1. svazek) učebnicové série „Propojování znalostí se životem“ od nakladatelství Vietnam Education Publishing House je definice obdélníku čtyřúhelník se 4 pravými úhly.

Vlastnosti obdélníku jsou, že má 2 rovnoběžné protilehlé strany, 2 stejné protilehlé strany, 2 stejné protilehlé úhly, 2 stejné úhlopříčky a protíná se ve středu každé přímky.

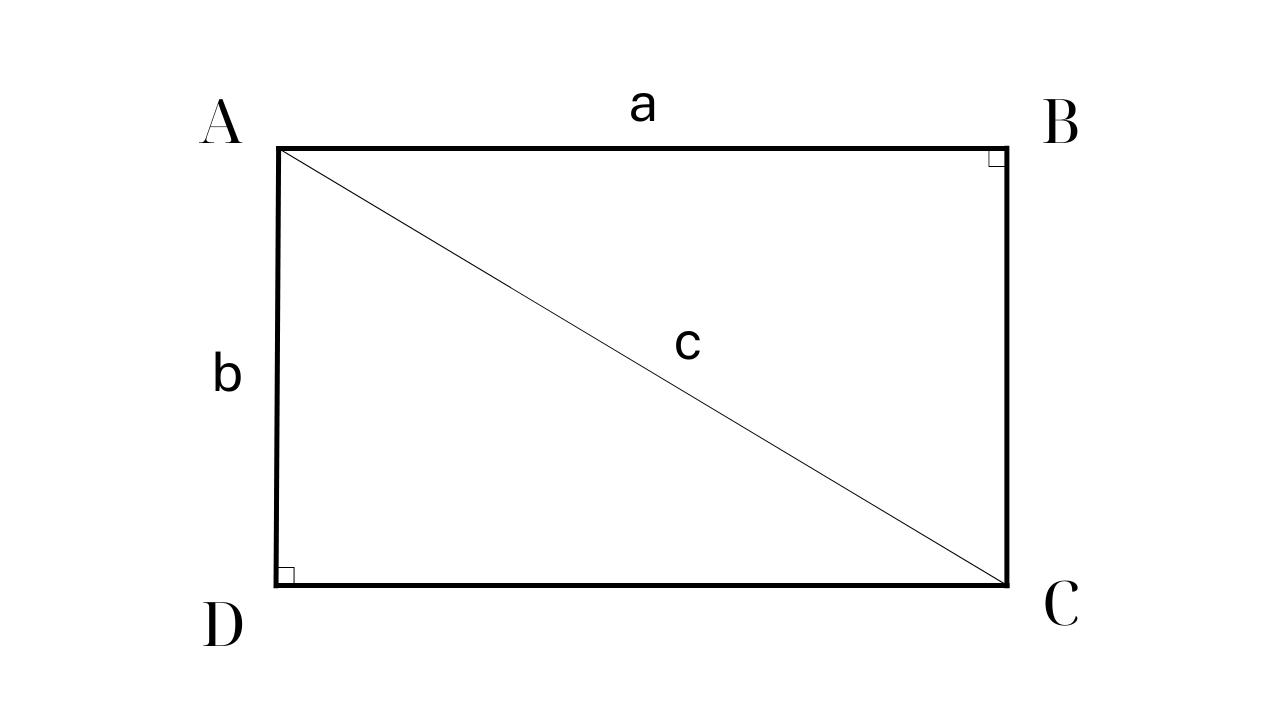
Vzorec pro výpočet plochy obdélníku

V lekci 52, matematický sešit 3 (svazek 2) z učebnicové série „Propojení znalostí se životem“ od nakladatelství Vietnam Education Publishing House je vzorec pro výpočet plochy obdélníku vynásobený délkou a šířkou (stejná měrná jednotka).

S = axb

Tam uvnitř:

S: Plocha obdélníku

a: Délka obdélníku

b: Šířka obdélníku

Například: Obdélníková dřevěná deska má šířku 5 cm a délku 15 cm. Vypočítejte plochu této dřevěné desky.

Odpověď: Plocha dřevěného prkna je: S = 5 x 15 = 75 ( ^cm² )

Vzorec pro výpočet plochy obdélníku, když je známa jedna strana a úhlopříčka.

Pro výpočet plochy obdélníku na základě jeho úhlopříčky a jedné strany je třeba zkombinovat Pythagorovu větu se základním vzorcem pro výpočet plochy.

Krok 1: Aplikujte Pythagorovu větu na pravoúhlý trojúhelník k výpočtu délky zbývající strany.

Krok 2: Použijte vzorec pro výpočet plochy obdélníku: S = axb

Příklad: Obdélník ABCD má AD = 60 cm a úhlopříčku AC = 100 cm. Vypočítejte obsah ABCD.

Odpověď:

Krok 1: Určete zbývající stranu obdélníku ABCD pomocí Pythagorovy věty v pravoúhlém trojúhelníku.

Proto: ^AC² = ^AB² + ^AD² => ^AB² = ^AC² - ^AD² = 10000 - 3600 = 6400 => AB = 80 (cm)

Krok 2: Plocha ABCD = AB x AD = 60 x 80 = 4800 ( ^cm² )

Vzorec pro výpočet plochy obdélníku při znalosti obvodu

Pro výpočet plochy obdélníku, když je znám obvod, je třeba zkombinovat vzorec pro výpočet obvodu a základní vzorec pro výpočet plochy.

Krok 1: Ze vzorce pro výpočet obvodu obdélníku, který je P = (a+b) x 2, kde P je obvod, a je délka, b je šířka obdélníku, máme a = (P/2) - b nebo b = (P/2) - a

Krok 2: Po nalezení a nebo b použijte vzorec pro výpočet plochy obdélníku: S = axb

Znamení k poznání obdélníku?

Podle učebnicové série „Propojení znalostí se životem“ pro lekci 13, matematiku 8 (1. díl) od nakladatelství Vietnam Education Publishing House jsou znaky pro rozpoznání obdélníku:

- Čtyřúhelník má 3 pravé úhly (na základě definice)

- Rovnoběžník má 1 pravý úhel

- Rovnoběžník má dvě stejné úhlopříčky.

- Rovnoramenný lichoběžník má jeden pravý úhel.

Je obdélník rovnoběžník?

Podle učebnicové série „Propojení znalostí se životem“ pro lekci 13, matematiku 8 (1. díl) od nakladatelství Vietnam Education Publishing House má obdélník všechny vlastnosti rovnoběžníku. Obdélník je tedy speciální rovnoběžník.

Je obdélník rovnoramenný lichoběžník?

Lekce 13, Matematika 8 (1. díl) Učebnicová série „Propojení znalostí se životem“ od nakladatelství Vietnam Education Publishing House, obdélník má všechny vlastnosti rovnoramenného lichoběžníku. Obdélník je tedy speciální formou rovnoramenného lichoběžníku.

(Syntetický)

Zdroj: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html